5 Easy Steps to Calculate Cpk in Excel
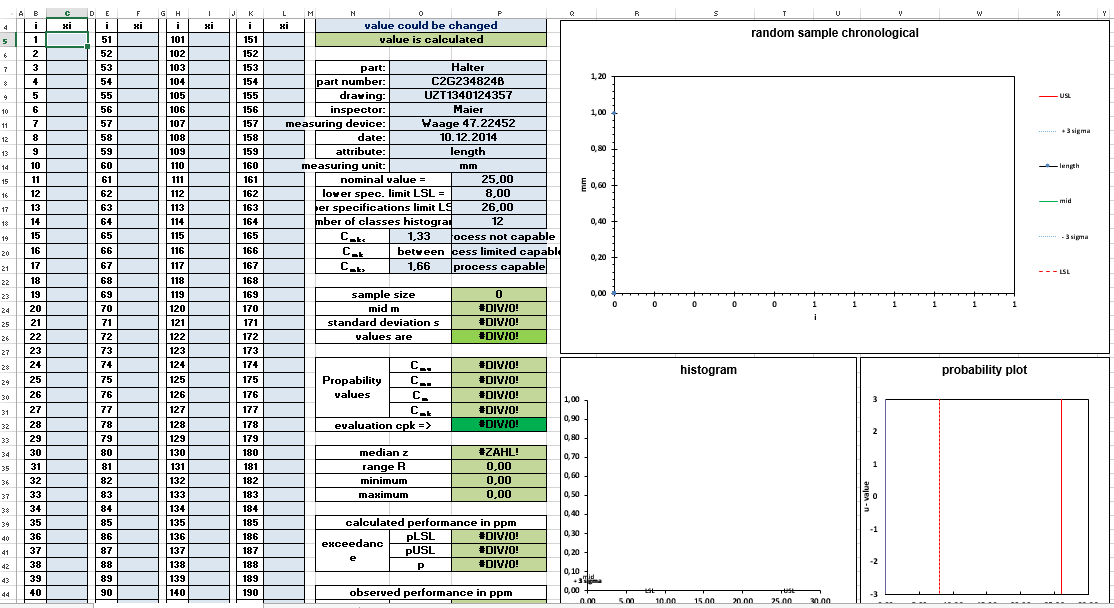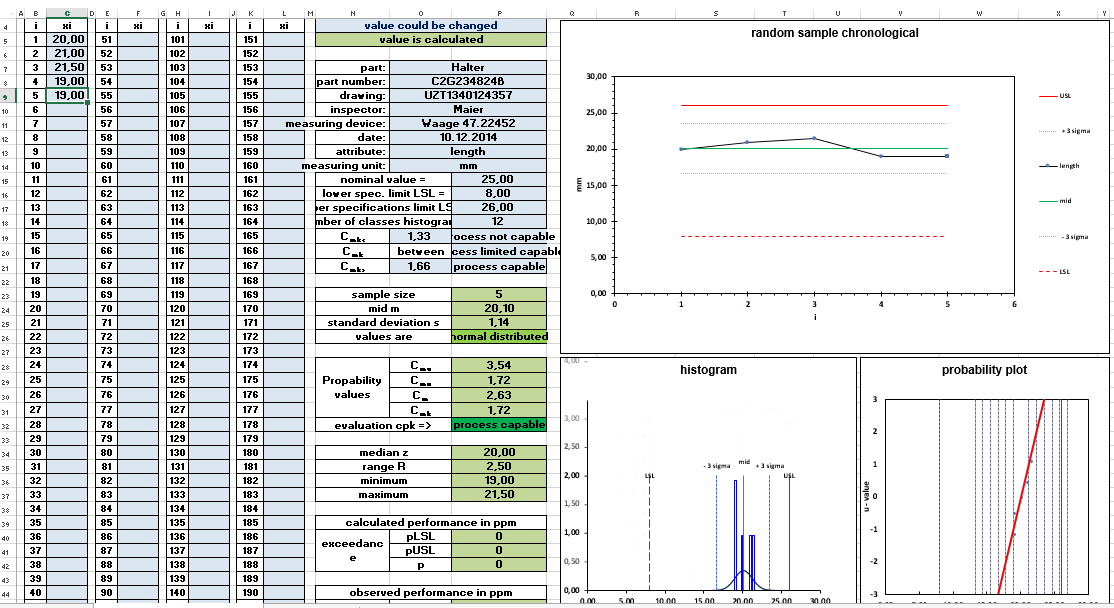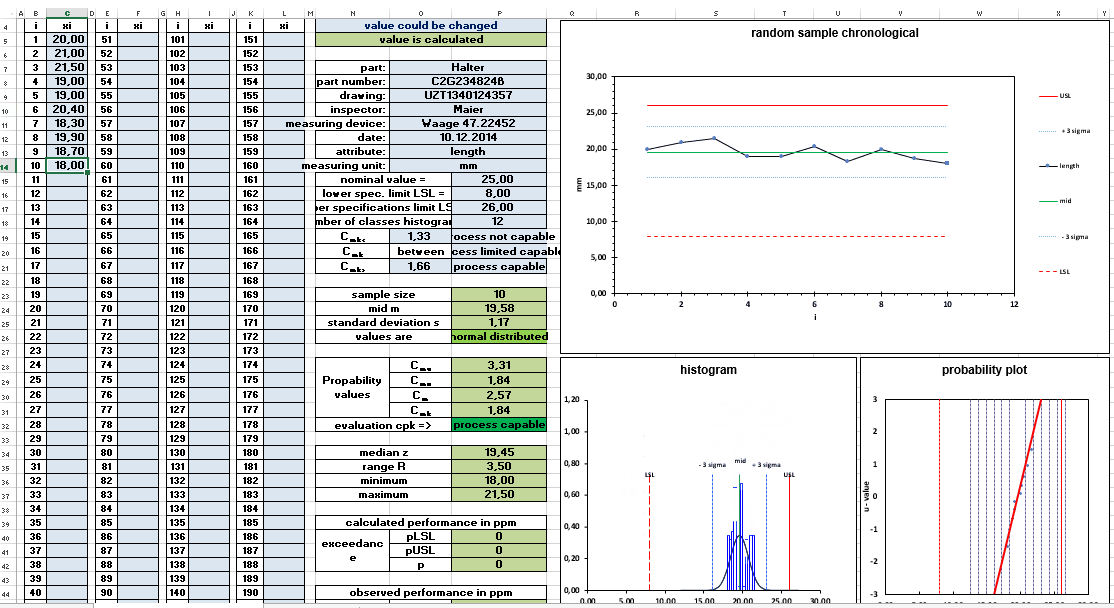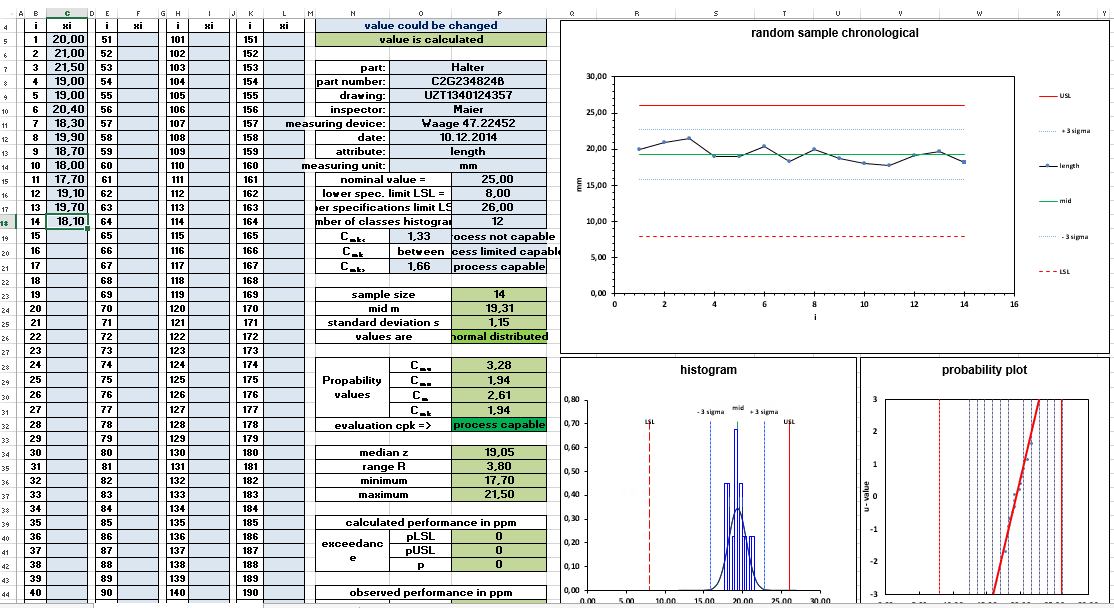
The Cpk (Capability Process Index) is a crucial metric used in Six Sigma and other quality management methodologies to measure how well a process is performing compared to its specification limits. If you're working in industries like manufacturing, pharmaceuticals, or any sector where process capability is pivotal, knowing how to calculate Cpk in Excel can enhance your ability to assess the performance and stability of your processes. Here, we walk through five easy steps to get your Cpk calculations done efficiently in Microsoft Excel.
Step 1: Collect and Organize Data


The first step in calculating Cpk in Excel is to gather all relevant data points from your process. Here’s what you need to do:
- Identify Measurement Points: Determine what part of your process you will measure. This could be the diameter of a manufactured part, the temperature in a cooling chamber, or any other measurable parameter.
- Sample Size: Collect a sufficiently large sample size. A minimum of 30 measurements is recommended to get a statistically significant result.
- Data Entry: Input these measurements into an Excel spreadsheet. Use columns to categorize data if necessary.
📝 Note: Ensure your data is clean, without duplicates or erroneous values, as these can skew your results.
Step 2: Calculate Process Mean and Standard Deviation

After collecting your data, you need to compute the process mean (μ) and the standard deviation (σ):
- Mean (μ): Use Excel’s
=AVERAGE(A1:A30)to find the mean value of your dataset, where A1 to A30 is your data range. - Standard Deviation (σ): Use the function
=STDEV.S(A1:A30)to calculate the standard deviation. This formula computes the sample standard deviation, which is preferred when working with a sample of the data rather than the entire population.
Step 3: Determine the Upper and Lower Specification Limits
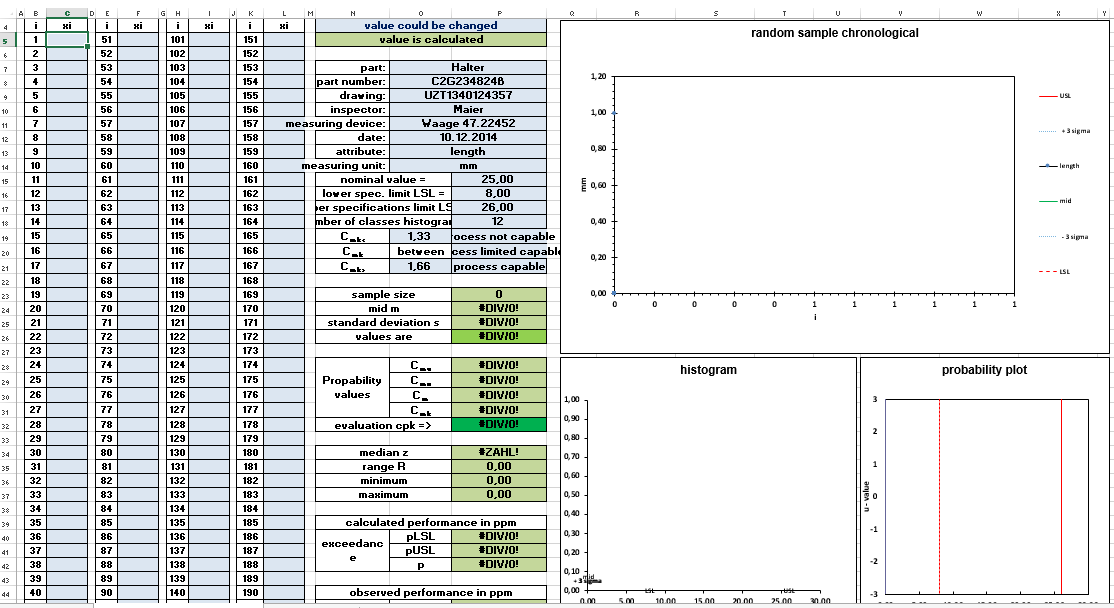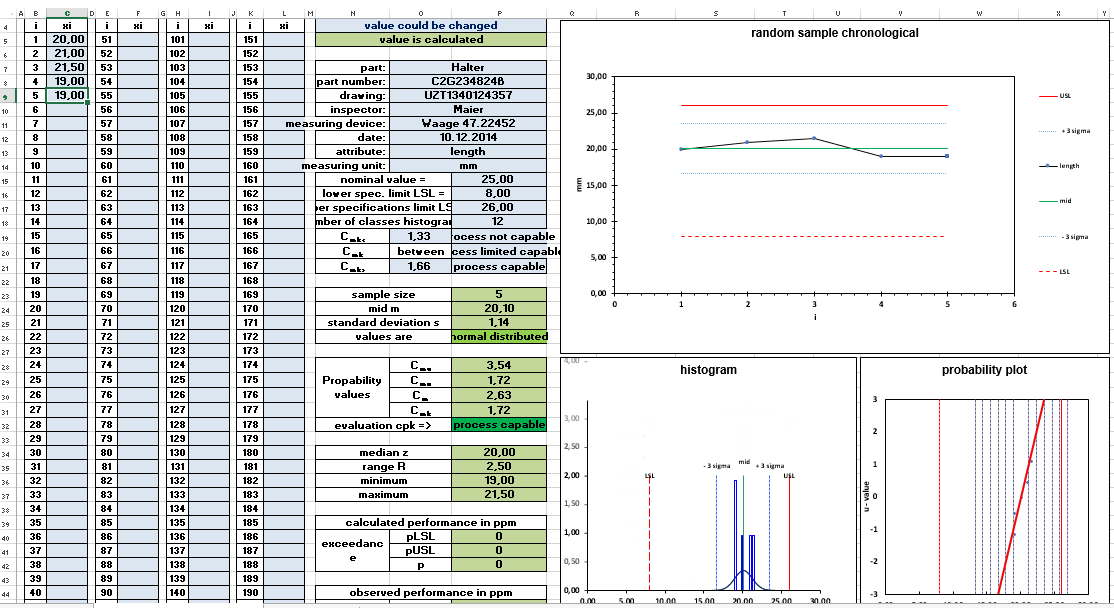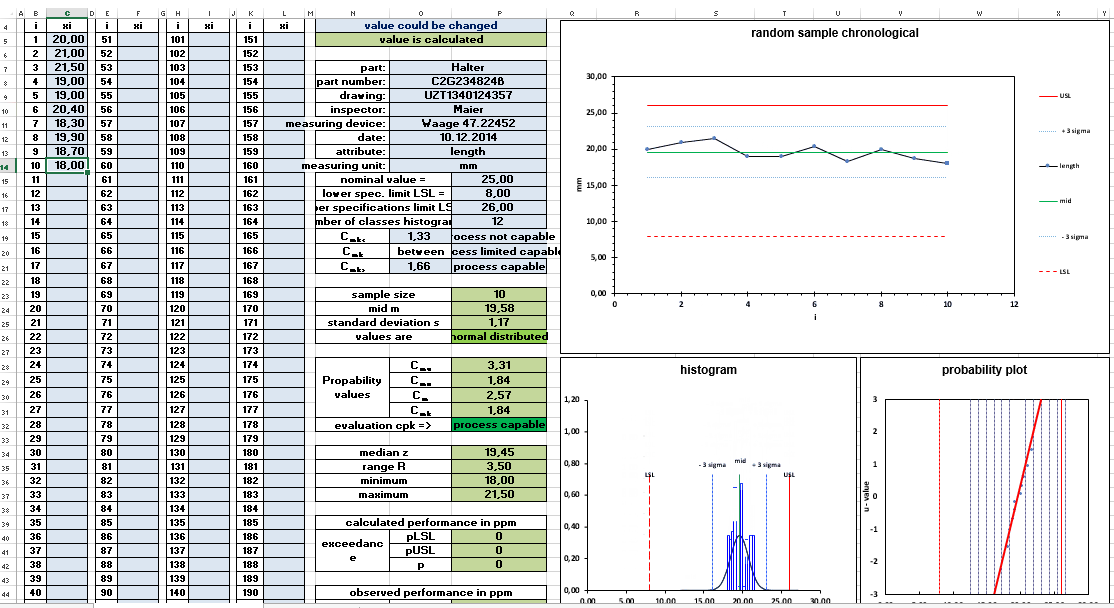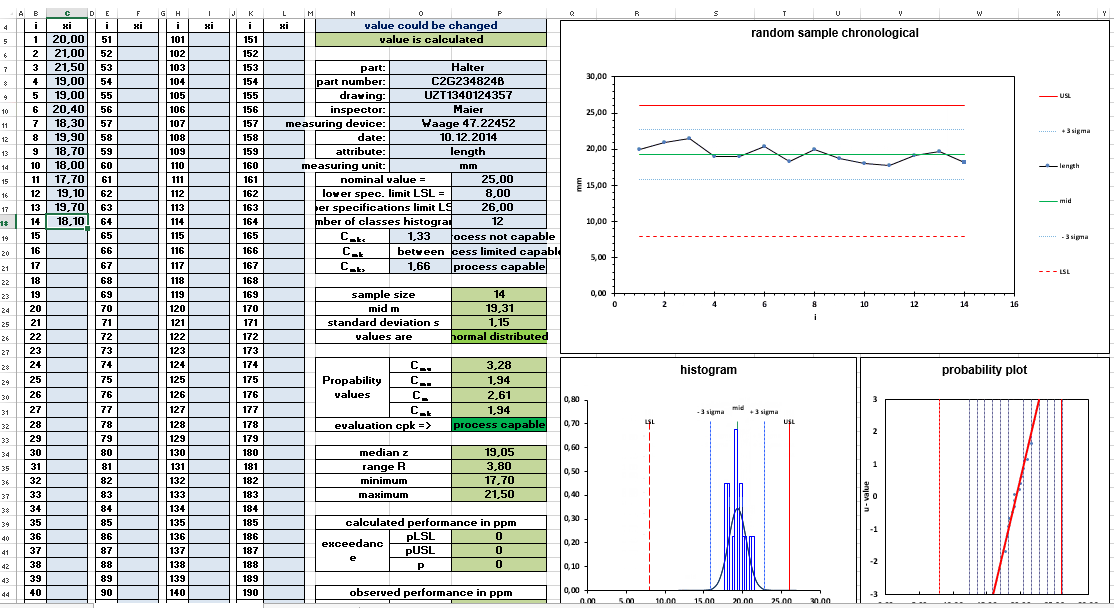

The upper and lower specification limits define the boundary within which your product or process should fall for it to be acceptable:
- Upper Specification Limit (USL): This is the highest acceptable value for your product or process. This could be a physical dimension, a tolerance range, or any other critical quality characteristic.
- Lower Specification Limit (LSL): The lowest acceptable value within your specification range.
Step 4: Compute the Process Capability Index (Cpk)

Now, with the data organized, mean, standard deviation, and specification limits set, let’s calculate Cpk:
- Cpk is defined as the lesser of the two indices:
- Cpu = (USL - μ) / (3σ)
- Cpl = (μ - LSL) / (3σ)
- Cpk = min(Cpu, Cpl)
You can calculate this in Excel as follows:
| Formula | Excel Formula |
|---|---|
| Cpu | =(B1-A1)/(3*A2) |
| Cpl | =(A1-B2)/(3*A2) |
| Cpk | =MIN(Cpu, Cpl) |
Step 5: Interpret the Results
Your Cpk value indicates:
- Cpk > 1.33: Your process is capable and meets specifications with high confidence.
- 1.0 < Cpk < 1.33: Process is capable but may require some improvement.
- Cpk < 1.0: The process is not capable, and immediate action is required to bring it within specifications.
🔍 Note: Remember, Cpk tells you if your process is capable but not if it is in control. Use control charts alongside Cpk to monitor process stability.
Having calculated the Process Capability Index in Excel, you have a powerful tool to assess and improve the quality of your processes. The steps outlined provide a foundational approach to not only meet customer expectations but also to drive continuous improvement in your organization's operations.
What does a Cpk value of 1.0 mean?

+
A Cpk value of 1.0 indicates that the process meets the minimum specification but is not considered very capable. There is a significant chance that defects could occur, and process improvement is recommended.
Can Cpk be negative?

+
No, Cpk cannot be negative. It is always a positive value or zero. If you get a negative result, it indicates an error in your calculation or data entry.
How often should Cpk be calculated?

+
It depends on the process stability. For stable processes, quarterly calculations might suffice, but for processes showing variability, monthly or even weekly calculations are advisable.