5 Easy Steps to Calculate P-Values in Excel

Understanding how to calculate p-values is essential for those working with data analysis, especially in fields like statistics, psychology, or medical research. P-values help determine the statistical significance of your findings, indicating whether the results are due to chance or represent a real effect. This guide will walk you through the process of calculating p-values in Microsoft Excel with these easy steps.
Step 1: Understanding P-Value and Statistical Hypothesis

Before diving into Excel’s functions, it’s crucial to grasp what a p-value signifies. The p-value represents the probability of obtaining test results at least as extreme as the observed ones, under the assumption that the null hypothesis is true. Here’s how you can frame your hypothesis:
- Null Hypothesis (H0): There is no effect or difference.
- Alternative Hypothesis (H1): There is an effect or difference.
Step 2: Choosing the Correct Statistical Test

The type of data you are working with will dictate which statistical test is appropriate. Here are some common scenarios:
- T-Test for comparing means of two groups.
- Z-Test when the population variance is known or sample size is large.
- Chi-Square Test for categorical data.
- ANOVA for comparing means of three or more groups.
Your choice will directly influence the formula or function you’ll use in Excel.
Step 3: Preparing Your Data

Ensure your data is formatted correctly in Excel:
- Label your columns clearly, like ‘Sample Size’, ‘Mean’, ‘Standard Deviation’, ‘Known Population Variance’ if applicable.
- Keep your data clean and in an organized manner to avoid calculation errors.
Example of data formatting:
| Sample Size | Mean | Standard Deviation |
|---|---|---|
| 25 | 48.7 | 4.2 |
| 30 | 52.3 | 5.1 |
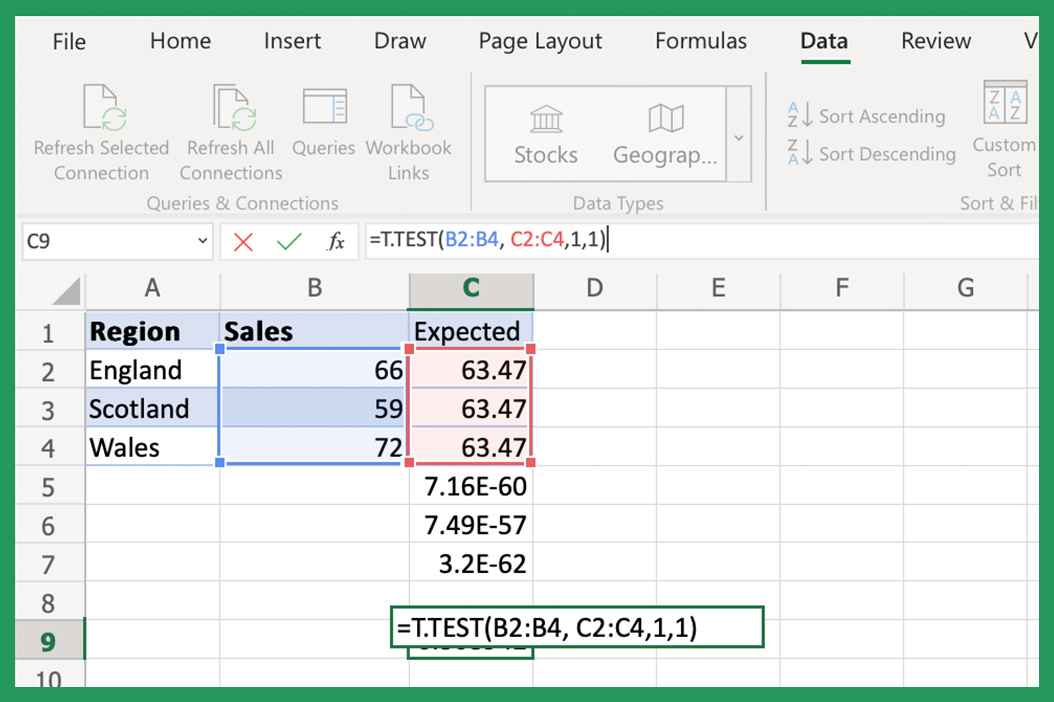
Step 4: Using Excel Functions to Calculate P-Values
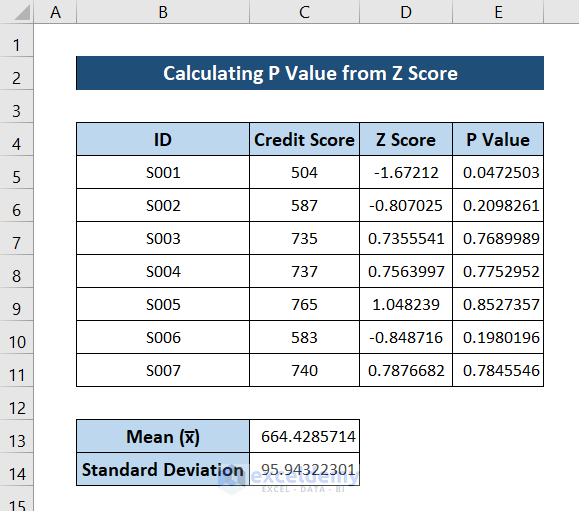
Here are some common functions in Excel to calculate p-values:
- For a T-Test, you can use
T.TESTfunction. Here’s how to use it:
T.TEST(array1,array2,tails,type)
Example:
=T.TEST(A2:A26, B2:B31, 2, 1)
📘 Note: array1 and array2 are your sample data, tails determines if you want a one-tailed or two-tailed test, and type indicates the type of t-test (1 for paired, 2 for two-sample equal variance, 3 for two-sample unequal variance).
Z.TEST function:Z.TEST(array,x,sigma)
Example:
=Z.TEST(A2:A26, B1, B2)
Step 5: Interpreting Your P-Value

After calculating your p-value, here’s what you should consider:
- A low p-value (typically below 0.05) indicates that your results are statistically significant, meaning there’s strong evidence against the null hypothesis.
- A high p-value suggests you cannot reject the null hypothesis, possibly indicating no significant effect or difference.
Remember, p-values alone do not measure the strength or importance of an effect; they merely suggest whether an effect might be present.
In summary, calculating p-values in Excel involves understanding your data, selecting the right test, properly preparing your dataset, using Excel's statistical functions, and interpreting the results. This approach allows you to make informed decisions based on your data analysis.
To enhance your understanding, here are some frequently asked questions related to calculating p-values in Excel:
What is the difference between a one-tailed and a two-tailed test?

+
A one-tailed test looks for an effect in one direction, either significantly larger or smaller, while a two-tailed test looks for any significant difference, regardless of direction.
Can I calculate p-values for non-normal data?
+
Excel’s built-in functions typically assume normality, but for non-normal data, you might need to use non-parametric tests like the Mann-Whitney U test or the Wilcoxon signed-rank test, which are available in certain statistical software.
What if my data is paired?

+
When dealing with paired data, use the paired t-test option (type = 1 in the T.TEST function) to account for the dependency between the samples.