5 Simple Steps to Calculate P Value in Excel

Understanding P-values in statistical analysis is crucial for anyone involved in research, data analysis, or even just learning about these topics. Excel, with its straightforward functions and calculations, provides an accessible platform for such computations. This guide walks through how to calculate the P-value in Excel using five simple steps, ensuring even beginners can perform this task with confidence.
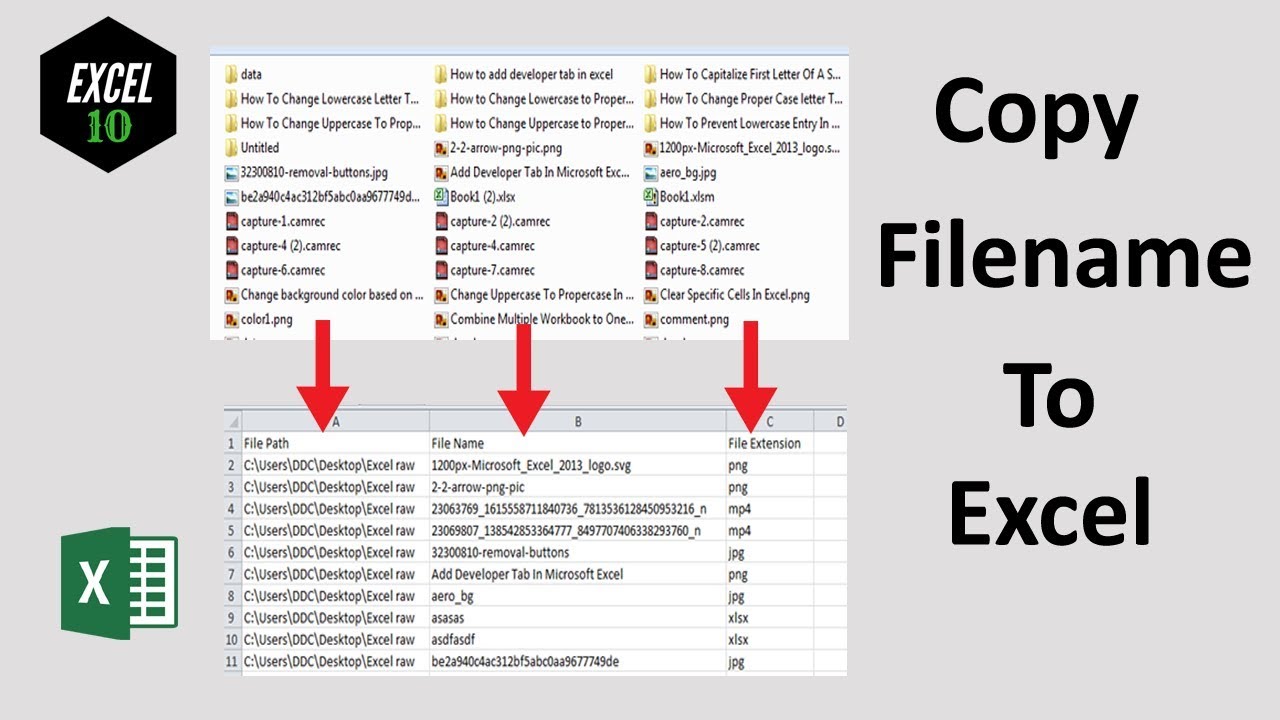
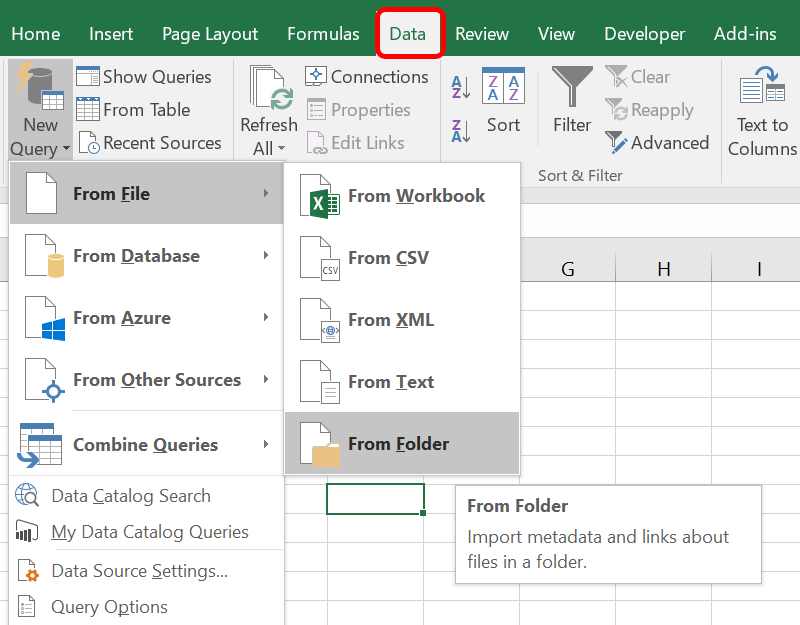
Step 1: Import Your Data

To start, you need data to analyze. Import your dataset into Excel. This could be:
- From an external source like a CSV file
- Manually entered data
- Existing data in an Excel sheet
📊 Note: Ensure your data is clean; there are no missing or extraneous values, as this can affect your results.
Step 2: Set Up Your Hypothesis
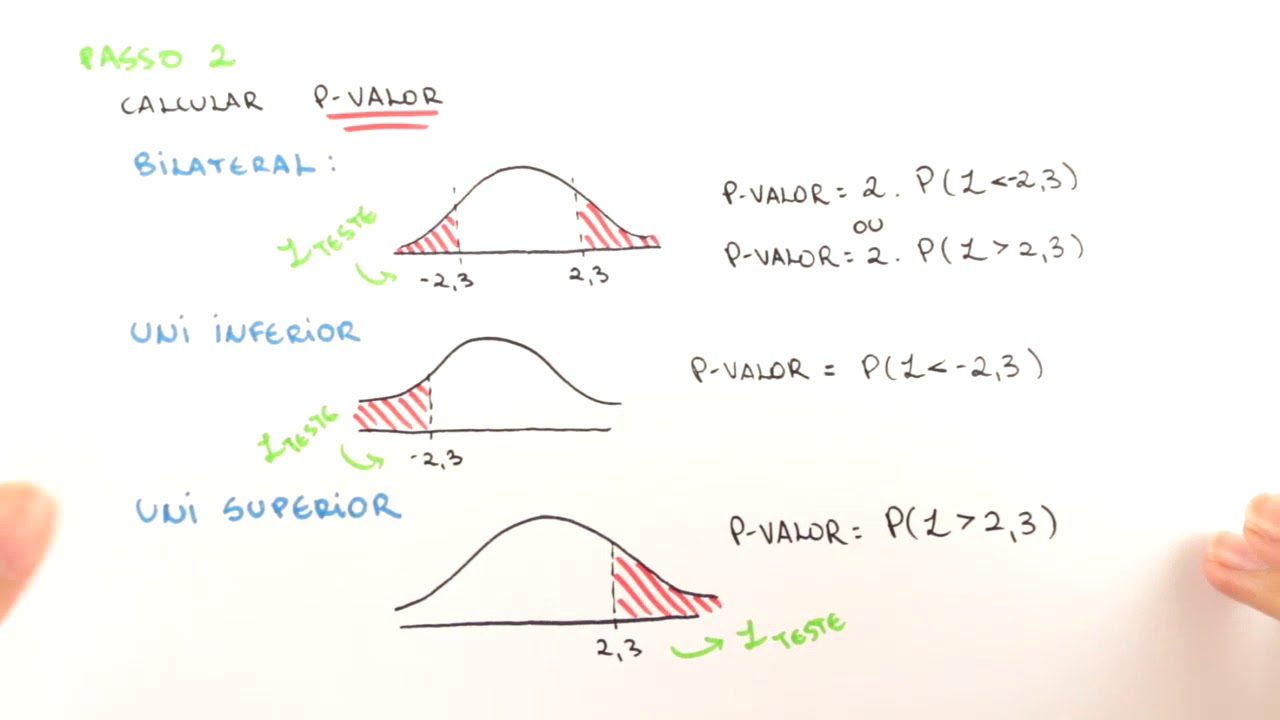
Before you calculate a P-value, you need a hypothesis:
- Null Hypothesis (H0): There is no significant difference or relationship between groups.
- Alternative Hypothesis (H1): There is a significant difference or relationship.
Choose an appropriate test based on your data type and question (e.g., t-test for comparing means, chi-square for categorical data).
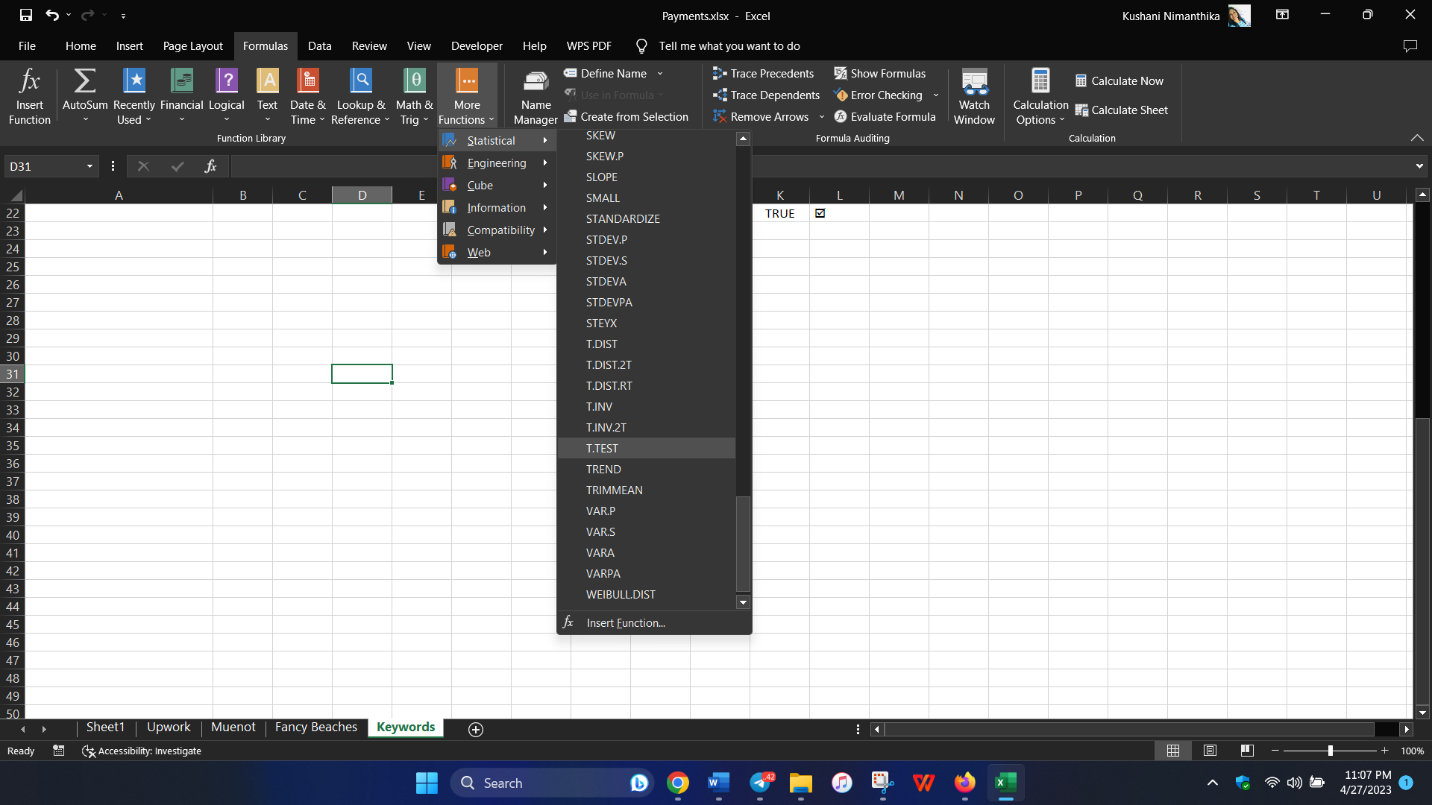
Step 3: Perform the Appropriate Statistical Test

Excel offers several built-in functions for statistical tests:
- T.Test: For two-sample t-tests.
- CHISQ.TEST: For chi-square tests.
- F.TEST: For F-tests to compare variances.
Here is how to use T.Test:
| Argument | Description |
|---|---|
| Array1 | First data set |
| Array2 | Second data set |
| Tails | Number of distribution tails (1 for one-tailed, 2 for two-tailed) |
| Type | Type of t-test (1 for paired, 2 for two-sample equal variance, 3 for two-sample unequal variance) |

Example: =T.TEST(A1:A10,B1:B10,2,3) where cells A1:A10 and B1:B10 contain your data.
Step 4: Interpret the P-Value
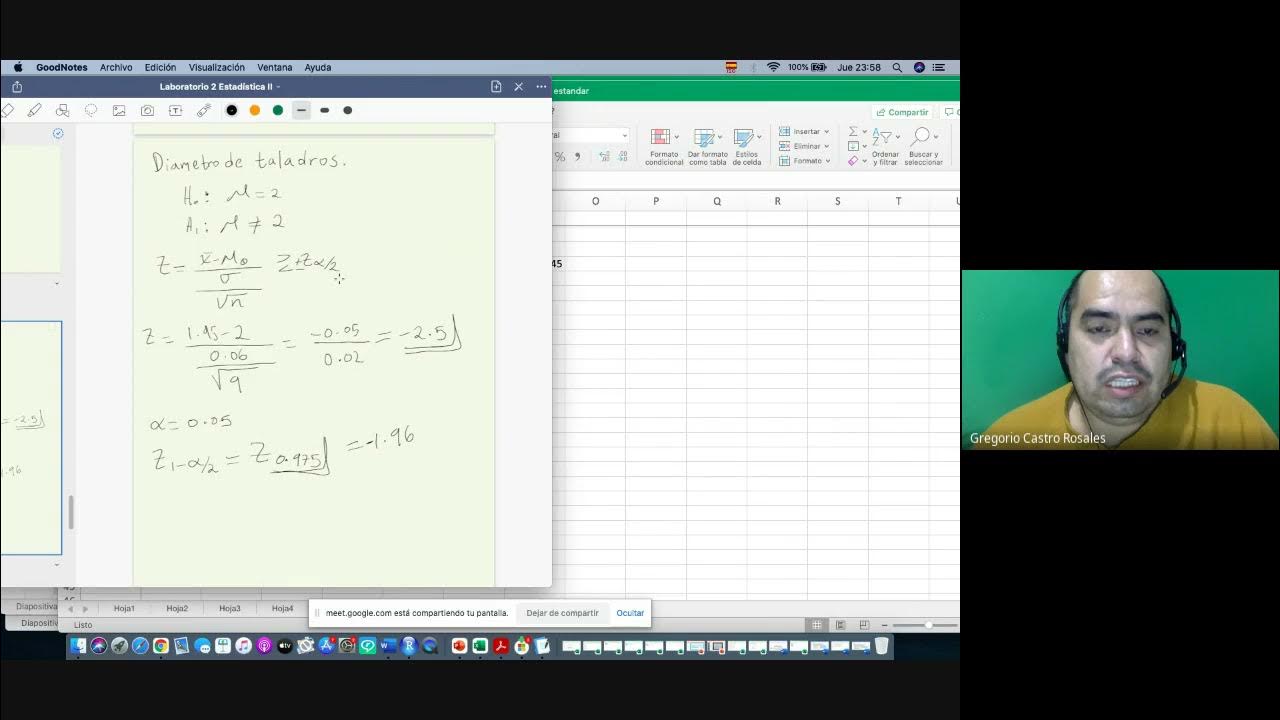
The output of the function gives you the P-value:
- If P-value < 0.05, reject the null hypothesis.
- If P-value > 0.05, fail to reject the null hypothesis.
Step 5: Make a Decision

Based on the P-value, decide whether there is sufficient evidence to support your alternative hypothesis. Remember, P-values give us the probability of obtaining results as extreme as the observed ones under the null hypothesis. They do not prove a hypothesis; they only inform us about the likelihood of our observations if the null hypothesis were true.
📝 Note: Statistical significance does not imply practical significance. Consider the effect size alongside the P-value.
Understanding P-Values
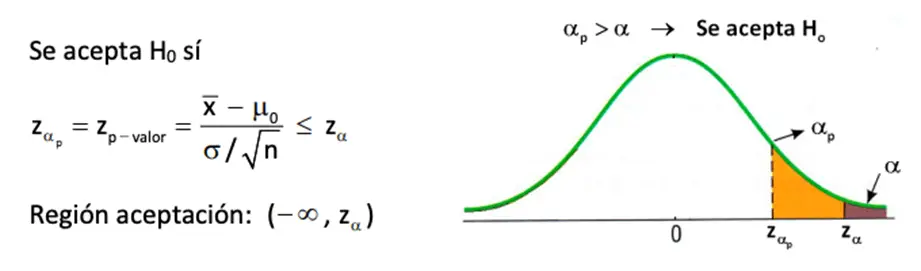
P-values indicate how probable it is to observe data like yours (or more extreme) assuming the null hypothesis is true. Here are some key points to remember:
- A smaller P-value does not necessarily mean your results are ‘better’ or ‘more true.’ It simply indicates stronger evidence against the null hypothesis.
- Always contextualize P-values with the study’s power, sample size, and the research question.
In wrapping up, this guide has covered the five simple steps to calculate P-value in Excel, from data import to hypothesis testing and decision-making. By following these steps, you can confidently use Excel to assess the significance of your data, making informed decisions in research, business, or academic settings. Remember to consider the broader implications of your findings beyond just the P-value, ensuring a holistic approach to data analysis.
What is the significance level in P-value testing?

+
The significance level (alpha) is typically set at 0.05. If the P-value is less than this, the result is statistically significant.
Can I calculate P-value for any statistical test in Excel?
+
Yes, Excel provides functions for various tests like t-tests, chi-square, and more, allowing you to calculate P-values for many common tests.
How does sample size affect P-value?

+
Sample size can impact P-value. Larger samples increase the power to detect smaller differences, potentially lowering the P-value even if the effect size is minimal.
What if my P-value is exactly 0.05?

+
This scenario indicates a borderline significance. In practice, you might still reject the null hypothesis, but it’s often a call for further investigation or a larger sample size.