Creating Excel Standard Curves Easily: A Step-by-Step Guide

In today's data-driven world, understanding how to effectively analyze and visualize data can be a game-changer for researchers, scientists, and business analysts alike. One of the most common data analysis techniques is the creation of standard curves, particularly in fields like chemistry, biology, and statistics. Excel, being widely available and intuitive, is a perfect tool for creating these curves. Here’s how you can create an Excel standard curve easily and efficiently.
What Are Standard Curves?
Before diving into the technical aspects, let’s briefly cover what standard curves are:
- Definition: A standard curve, also known as a calibration curve, is a graphical representation of a relationship between known concentrations of a substance and the corresponding response (e.g., absorbance, fluorescence).
- Purpose: They are used to quantify unknown samples by comparison against known standards.

Collecting Data for Your Standard Curve
Here’s how to gather the necessary data:
- Concentration: Determine the range of concentrations you want to measure.
- Response: This could be absorbance, fluorescence intensity, or any other measurable response relevant to your experiment.
Creating a Standard Curve in Excel
Follow these steps to create your standard curve:
- Open Excel: Start a new spreadsheet.
- Input Data: In columns A and B:
- Column A: List your known concentrations.
- Column B: Add the corresponding responses.
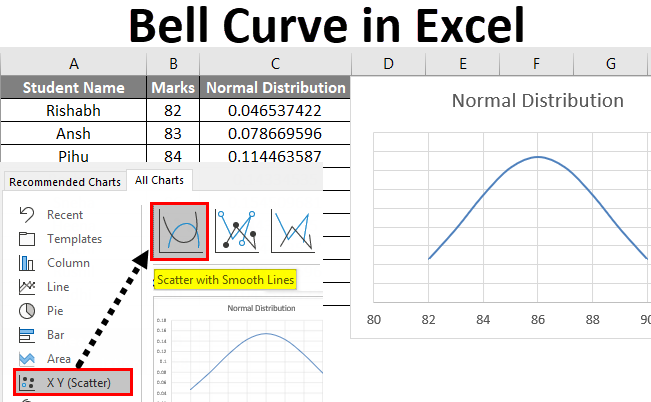
- Create a Chart:
- Select your data.
- Go to the ‘Insert’ tab.
- Select ‘Scatter Plot with Smooth Lines’ for your chart type.
- Add Trendline:
- Click on the chart.
- Go to Chart Tools > Design > Add Chart Element > Trendline > More Trendline Options.
- Choose the type of regression that best fits your data (linear, polynomial, etc.).
- Check ‘Display Equation on Chart’ and ‘Display R-Squared Value on Chart’ for detailed analysis.
⚠️ Note: Always check the R-squared value to assess the accuracy of your curve. An R² close to 1 indicates a good fit.
Interpreting Your Standard Curve
Understanding what your standard curve tells you is key to its effectiveness:
- Equation: The equation on the chart can be used to calculate the concentration of unknowns.
- R-squared: This statistical measure indicates how well your observed values fit a linear model.
| Curve Analysis | High R² | Low R² |
|---|---|---|
| Implication | Good model fit, reliable quantification | Poor model fit, data might not be linear or have other issues |

Common Pitfalls and Tips
Here are some common mistakes and tips for success:
- Range: Ensure your standard range encompasses the expected concentration of your unknowns.
- Outliers: Check for and address outliers, as they can skew your curve.
- Interpolation vs. Extrapolation: Only interpolate within the range of standards; extrapolation can lead to inaccurate results.
🔍 Note: For better accuracy, consider preparing standard solutions in replicates to minimize errors.
In sum, creating a standard curve in Excel can be streamlined into these key points:
- Data collection is paramount; ensure your concentration ranges and responses are accurate.
- The right chart type, in this case, a scatter plot, simplifies the process.
- Adding and interpreting the trendline gives you the tools needed for quantification.
- Awareness of common issues helps in troubleshooting your analysis.
How many points should I use for my standard curve?
+
At least three points are necessary for a basic curve, but 5 to 10 points will give a more robust curve with better reliability.
Can I use a non-linear regression for my standard curve?

+
Yes, if the relationship between concentration and response is not linear, Excel can fit polynomial, logarithmic, or other regression models as needed.
What is the significance of R-squared?
+
The R-squared value measures how closely your data points fit the trendline. The closer to 1, the better the fit, indicating your curve is likely to accurately predict unknown concentrations.