Calculate Degrees of Freedom in Excel Easily
In the realm of data analysis and statistical testing, understanding and calculating degrees of freedom (df) is crucial. Degrees of freedom essentially refer to the number of independent values or quantities which can be assigned to a statistical distribution. This concept plays a significant role when performing hypothesis tests, confidence interval calculations, and several other statistical procedures. In this blog post, we will explore how you can calculate degrees of freedom in Excel with ease, providing step-by-step guidance and highlighting why this calculation is important in various analytical contexts.
Understanding Degrees of Freedom
Before diving into the calculations, let's understand what degrees of freedom represent:
- Definition: The number of values in a data set that are free to vary after certain restrictions have been applied.
- Importance: It's crucial for determining the critical values in statistical tests, like t-tests, chi-square tests, and F-tests, affecting the results' validity and reliability.
- Example: For a sample of size n, if the mean is fixed, only n-1 values are free to vary because the last value is determined by the others to ensure the mean remains constant.
💡 Note: The degrees of freedom are often different depending on the statistical test you're performing.
Calculating Degrees of Freedom in Excel
Simple Sample Degree of Freedom
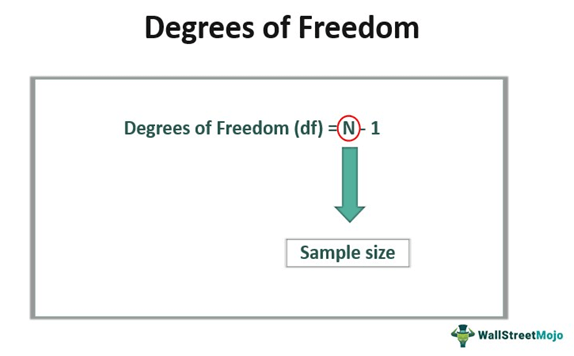
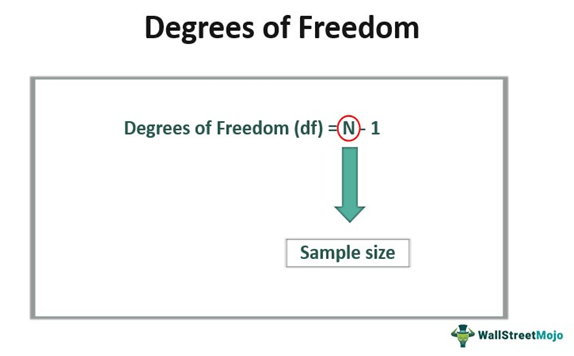
The most straightforward calculation of degrees of freedom is for a simple random sample:
df = n - 1Where n is the sample size.
To calculate this in Excel:
- Enter your sample size in cell A1.
- In another cell (let’s say B1), enter the formula:
=A1 - 1
This will give you the degrees of freedom for your sample.
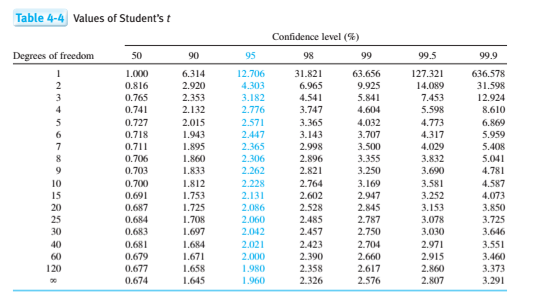
Degrees of Freedom in T-Tests
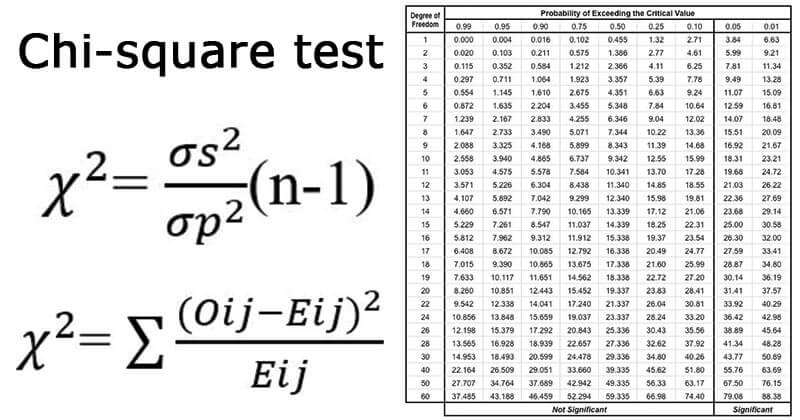
For a t-test, the degrees of freedom calculation can become slightly more complex:
- One-sample t-test: df = n - 1
- Two-sample t-test: df = n1 + n2 - 2 (where n1 and n2 are the sizes of the two samples).
Here's how to do it in Excel:
| Scenario | Formula |
|---|---|
| One-sample t-test | =n - 1 |
| Two-sample t-test | =n1 + n2 - 2 |

Assuming your sample sizes are in cells A1 and A2 for one and two-sample tests respectively:
- Use the formula
=A1 - 1for one-sample t-test. - For the two-sample t-test, enter
=A1 + A2 - 2in cell B1.
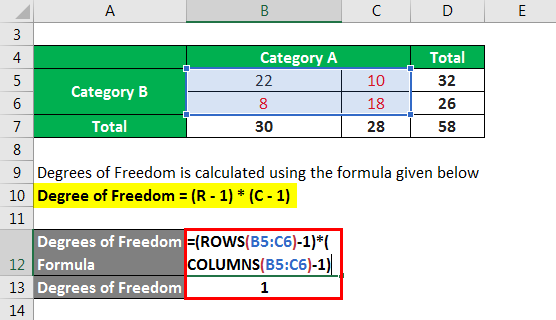
Chi-Square Test Degrees of Freedom

For the chi-square test, the degrees of freedom are calculated based on the number of categories in your data:
df = (r - 1) * (c - 1)Where r is the number of rows and c is the number of columns in your contingency table.
To calculate this in Excel:
- Enter the number of rows in cell A1 and the number of columns in cell B1.
- In another cell (like C1), type the formula:
=(A1 - 1) * (B1 - 1).
Conclusion

Mastering the calculation of degrees of freedom in Excel empowers you to perform statistical analyses with greater accuracy. By following the steps outlined above, you can easily compute degrees of freedom for different statistical tests, ensuring your data analysis is robust and valid. Remember, understanding the degrees of freedom not only helps in performing these tests correctly but also in interpreting the results appropriately, thereby enhancing the quality of your research and decision-making.
Why do degrees of freedom matter in statistical testing?

+
Degrees of freedom are crucial as they determine the shape of statistical distributions used for hypothesis testing. They influence the critical values which decide whether to reject or accept a null hypothesis, impacting the test’s power and accuracy.
Can degrees of freedom be negative?
+
No, degrees of freedom cannot be negative. If you encounter a situation where df seems negative, it indicates an error in your calculation or misunderstanding of the scenario, such as having more parameters to estimate than data points to estimate them from.
How does changing the sample size affect degrees of freedom?

+
Increasing the sample size increases the degrees of freedom. For example, in a one-sample t-test, df = n - 1, so with a larger n, you get more degrees of freedom, which generally means more power for your statistical tests.