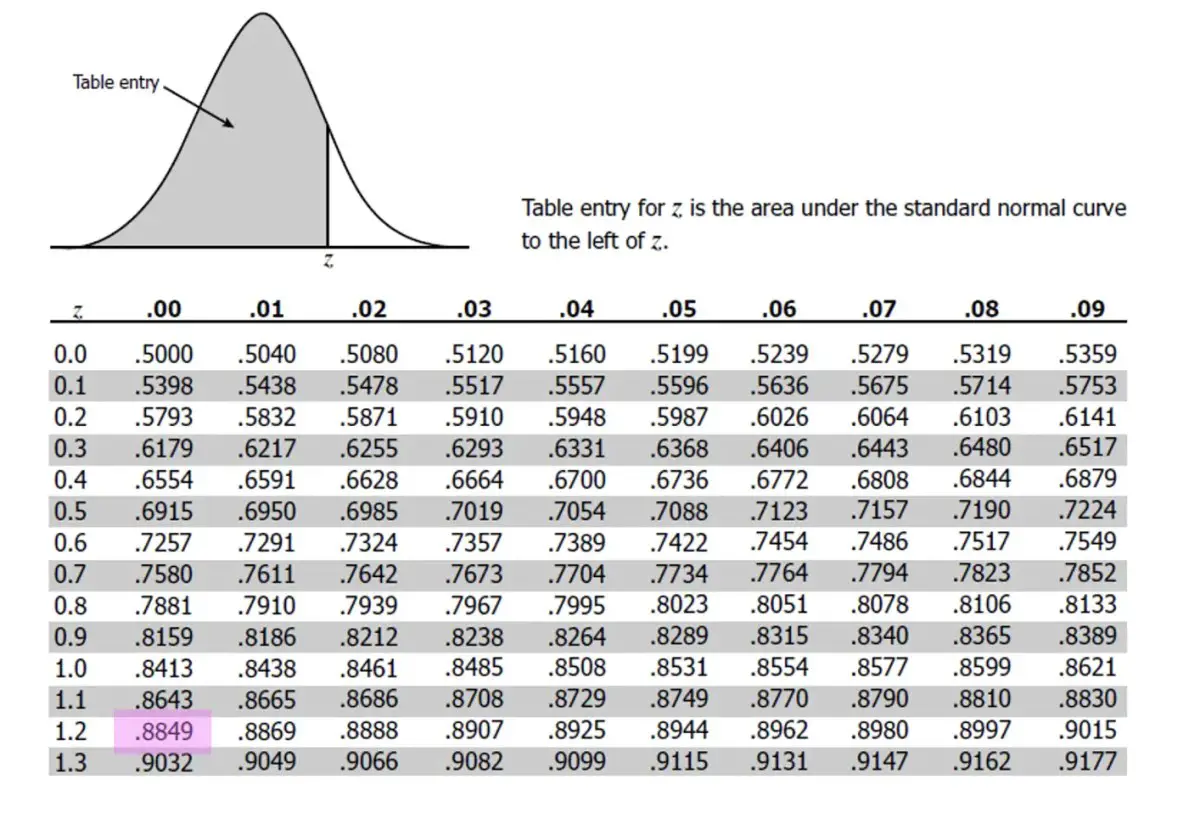
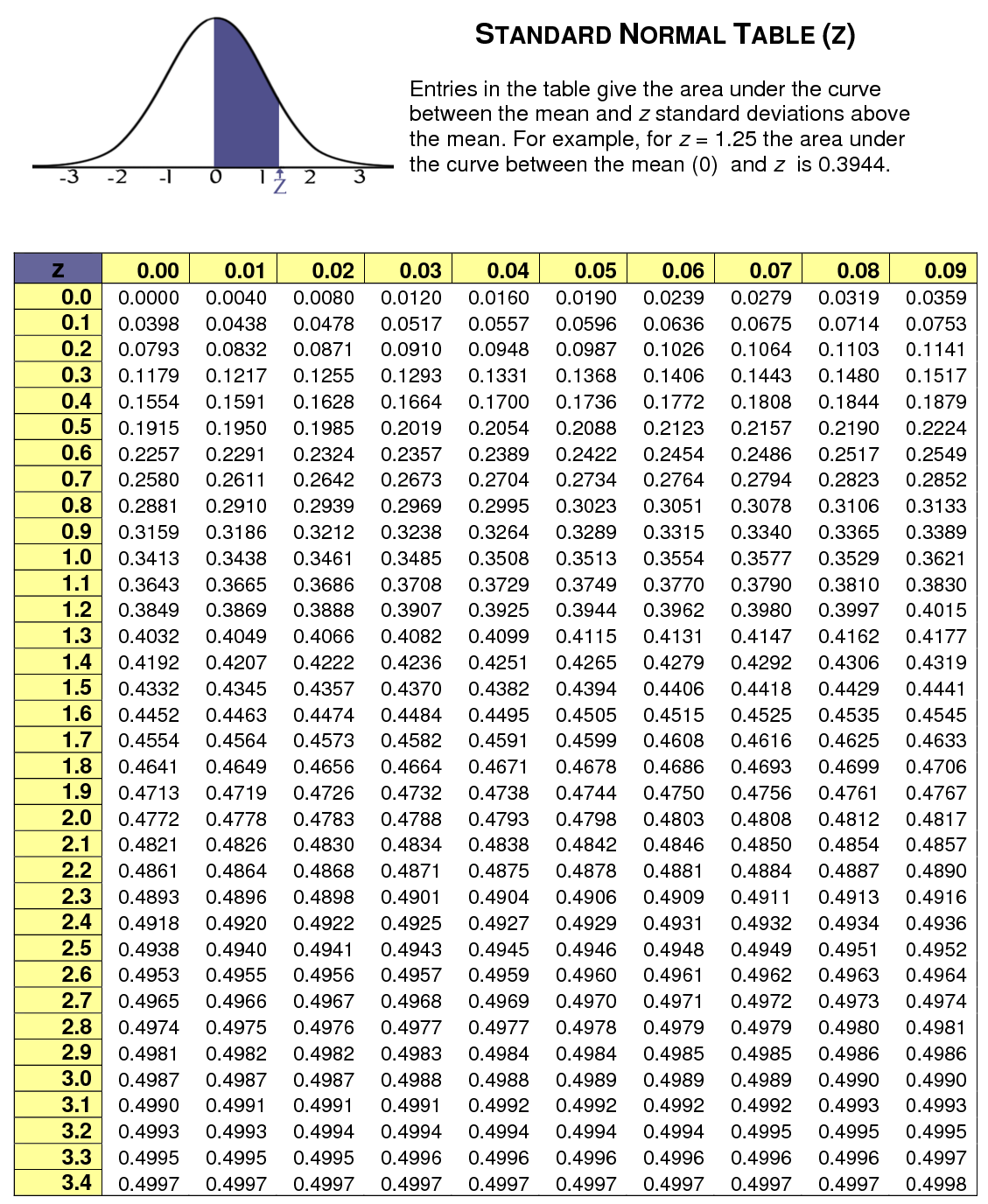
Calculate Z-Scores in Excel Easily: Step-by-Step Guide
Understanding statistical distributions is crucial for data analysis, and one of the most fundamental tools for this is the Z-score. The Z-score, or standard score, allows you to compare data points from different normal distributions by transforming them into a common scale. This step-by-step guide will walk you through how to calculate Z-scores in Microsoft Excel effortlessly.
What is a Z-Score?
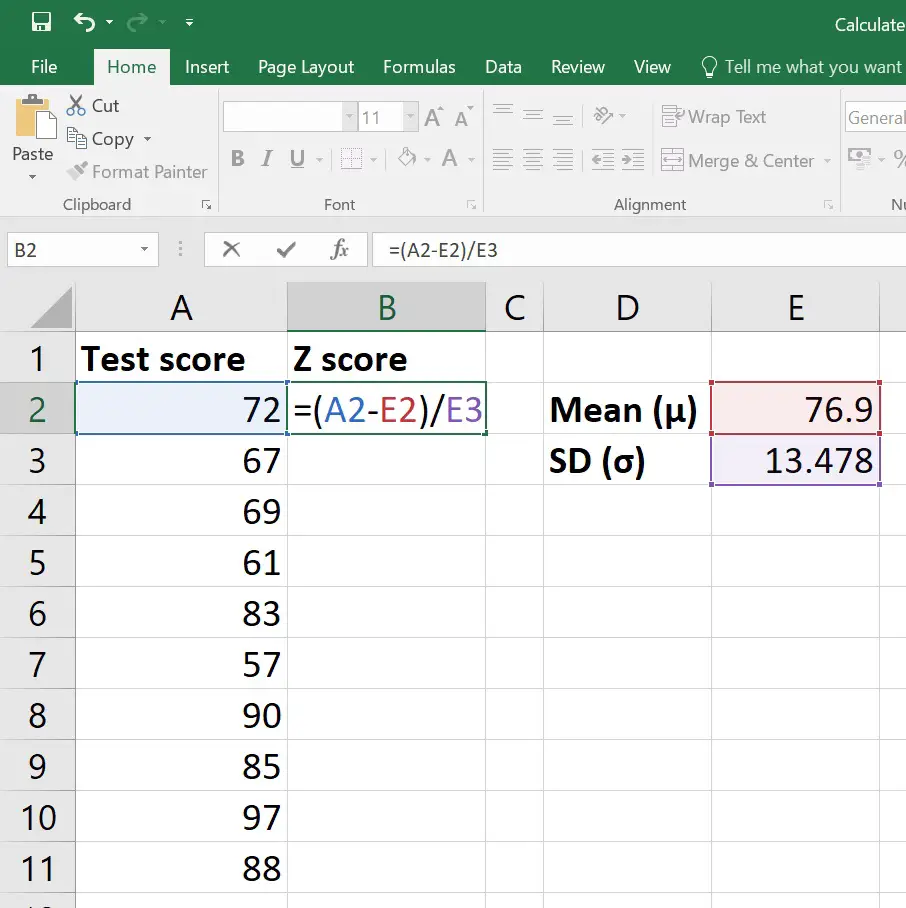
A Z-score tells you how many standard deviations a particular data point is away from the mean of a dataset. Here's the formula for calculating a Z-score:
[ Z = \frac{(X - \mu)}{\sigma} ]
- X: The value from your dataset
- μ: The mean of the dataset
- σ: The standard deviation of the dataset
Why Calculate Z-Scores?
Z-scores are incredibly useful for several reasons:
- They allow you to understand the position of a data point relative to the rest of the data.
- They enable comparisons between different datasets or scales.
- Z-scores are used in various statistical tests and procedures, like hypothesis testing and creating probability distributions.
Steps to Calculate Z-Scores in Excel
Here's how you can calculate Z-scores in Excel:
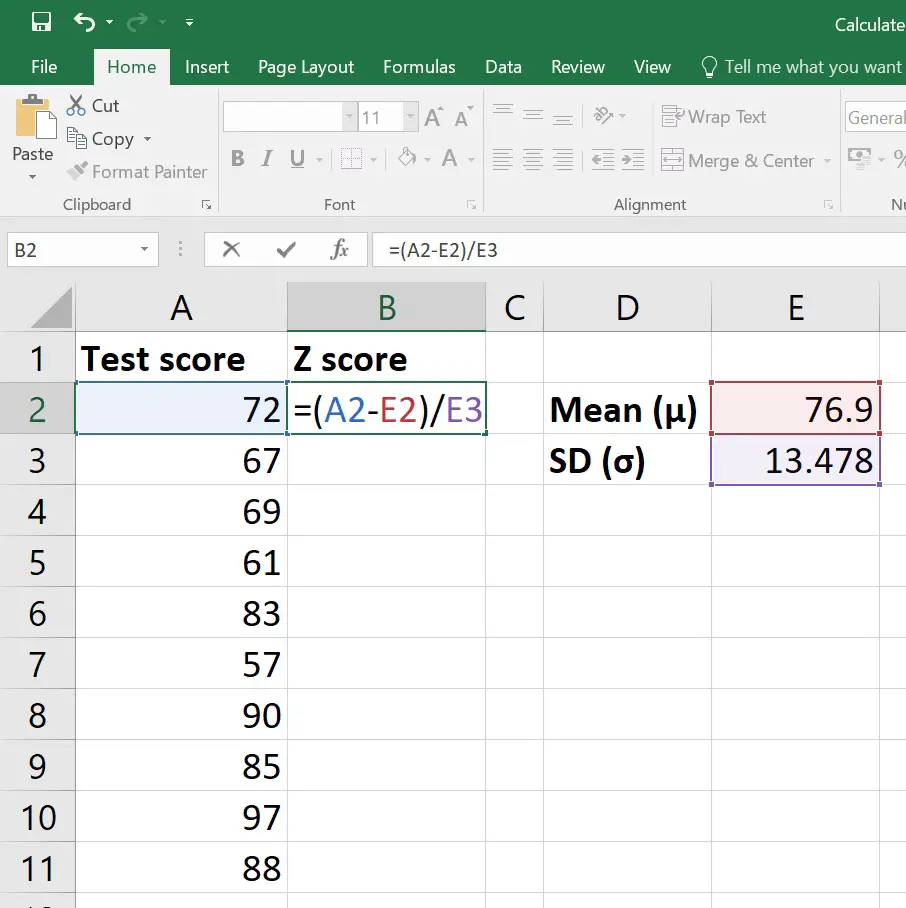
1. Enter Your Data
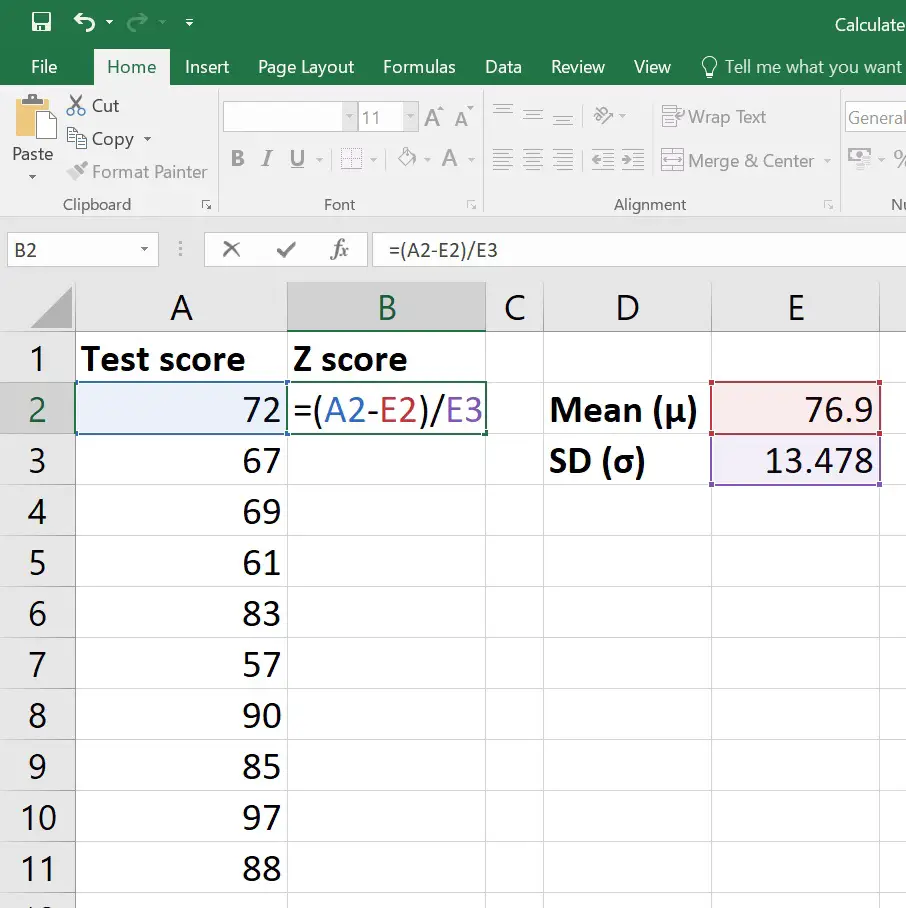
Start by entering your dataset into an Excel worksheet. Let's assume your data is in cells A1:A10.
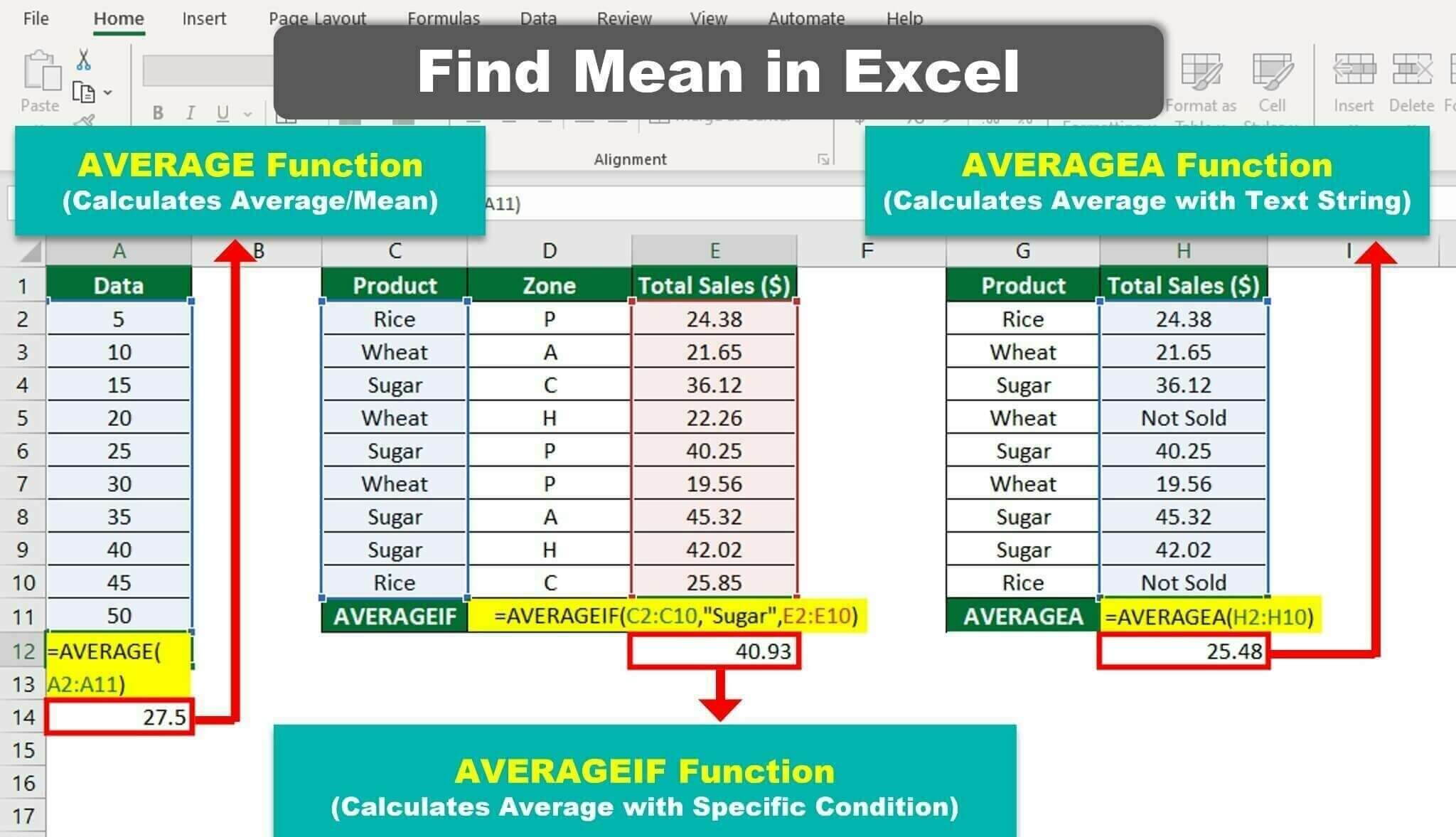
2. Calculate the Mean
Use the AVERAGE function to find the mean of your data. In cell B1, you might enter:
=AVERAGE(A1:A10)
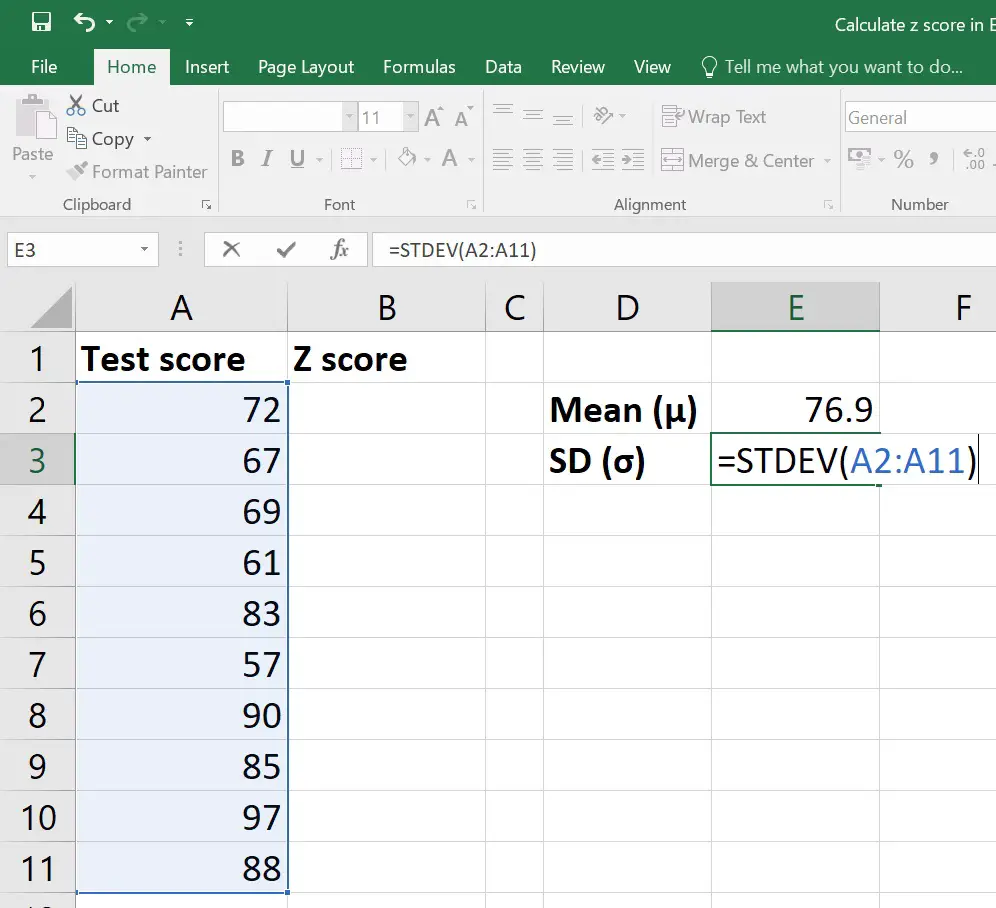
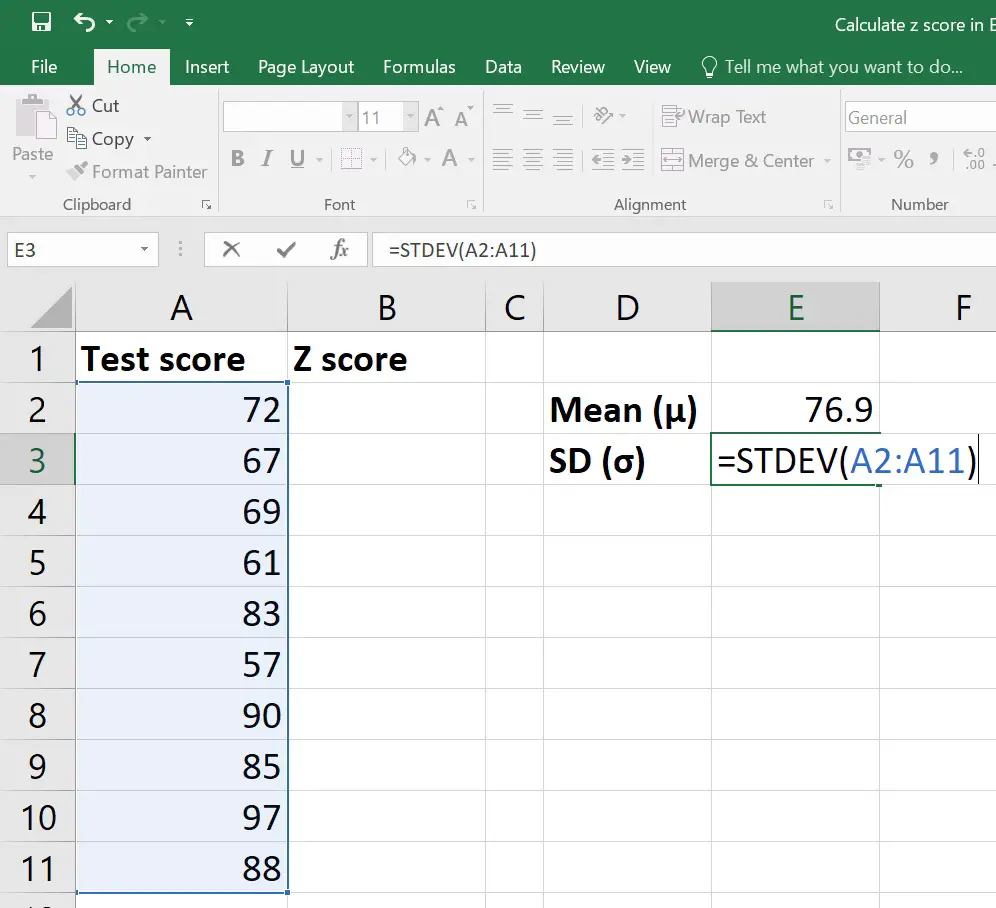
3. Calculate the Standard Deviation
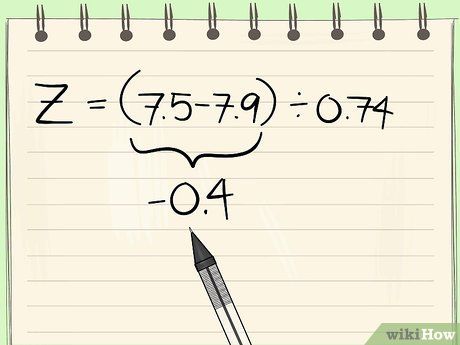
Next, calculate the standard deviation using the STDEV.S function for a sample or STDEV.P for a population. For this example, let's assume we're working with a sample:
=STDEV.S(A1:A10)
Enter this formula into cell C1.
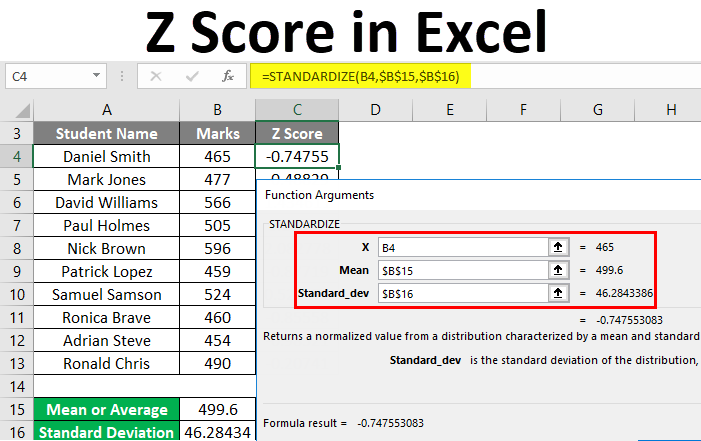
4. Compute the Z-Scores
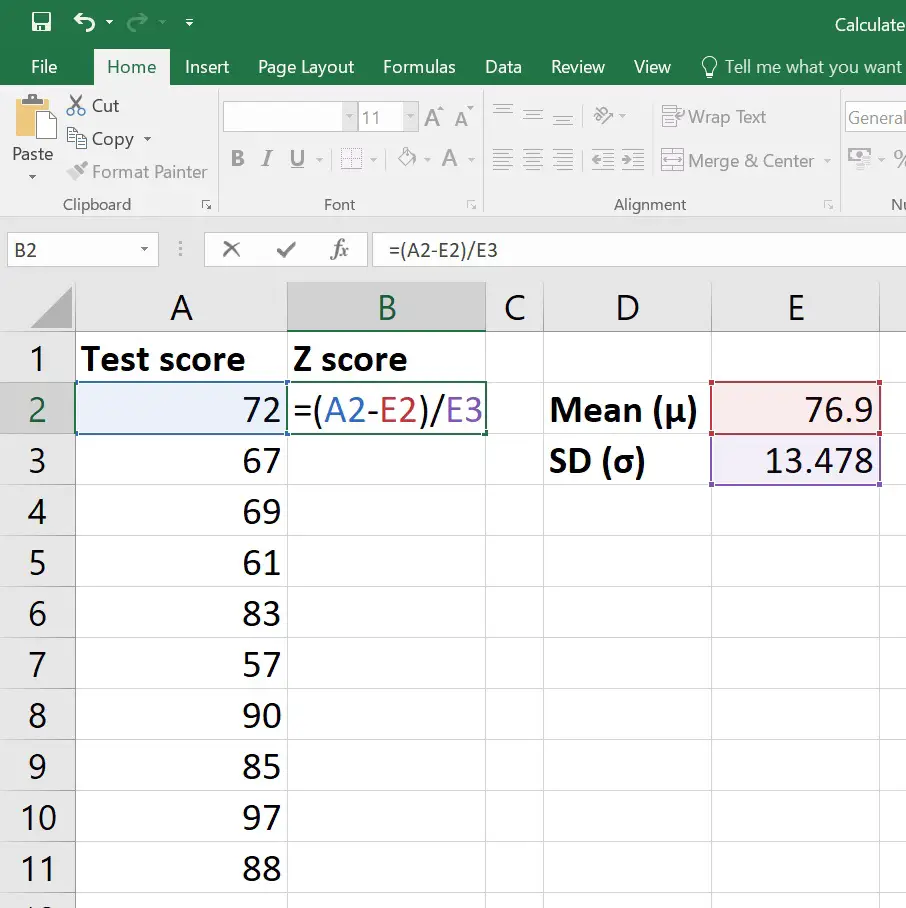
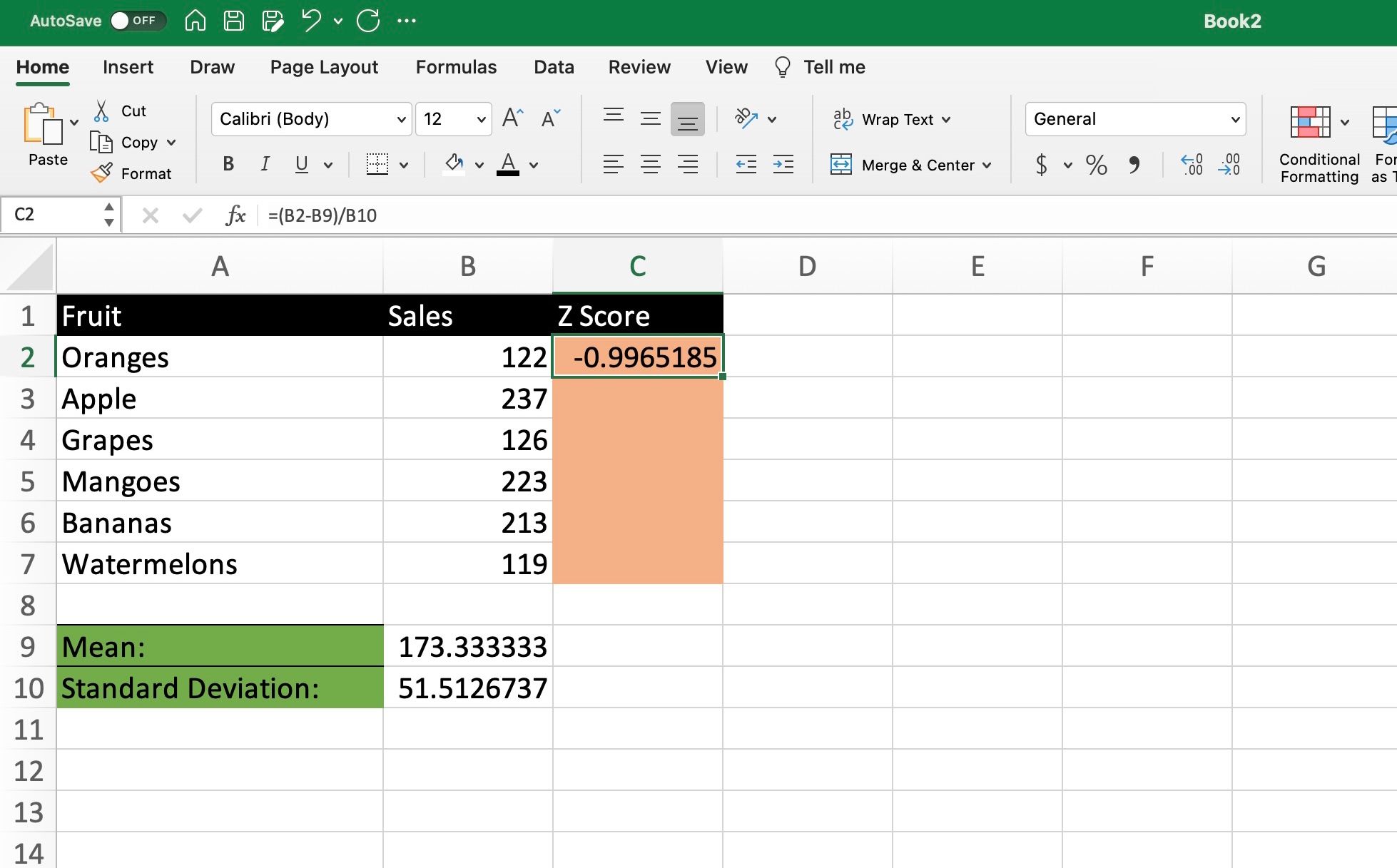
Now, we can compute the Z-scores for each data point in the dataset. In cell D1 (assuming your data starts from row 2), you would type:
=(A2-B1)/C1
Then, drag this formula down to fill the rest of the cells in column D.
5. Review Your Results
Your Z-scores are now calculated in column D. Here's a small excerpt to show what this might look like:
| Data Point | Mean | Std. Dev | Z-Score |
|---|---|---|---|
| 23 | 20 | 5 | 0.60 |
| 18 | 20 | 5 | -0.40 |
💡 Note: Always double-check the formula references when copying down, as absolute references ($B$1, $C$1) prevent the cell references from changing as you drag the formula.
Using Z-Scores for Data Analysis
Once you've calculated the Z-scores, here are some ways you can use them:
- Identifying Outliers: Data points with Z-scores far from 0 (commonly >3 or <-3) can be considered outliers.
- Data Normalization: Z-scores can normalize your data for comparisons or further statistical analysis.
- Probability Estimation: Knowing the Z-score allows you to estimate the probability of a data point occurring within a normal distribution.
To summarize, calculating Z-scores in Excel is straightforward once you understand the process. You can now easily standardize your data, identify outliers, and perform comparative analysis. Remember to keep your dataset up to date and always verify the accuracy of your calculations before making any conclusions or taking further actions based on the data.
What does a negative Z-score mean?

+
A negative Z-score indicates that the data point is below the mean. The further the Z-score is from zero, the farther the value is from the mean in a negative direction.
Can Z-scores be greater than 3?
+
Yes, Z-scores can exceed 3. However, data points with Z-scores of this magnitude are often considered outliers or rare events within a normal distribution.
How can Z-scores help in comparing different datasets?
+
By converting data points into Z-scores, you can compare different datasets even if they have different scales or units of measurement, as Z-scores reflect how many standard deviations a value is from the mean.