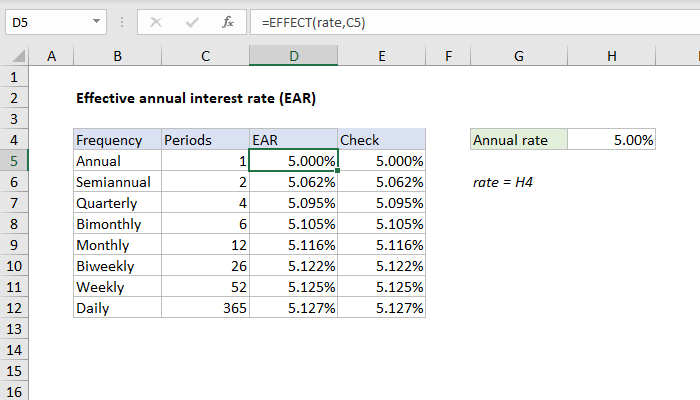
Understanding the Importance of Effective Interest Rate
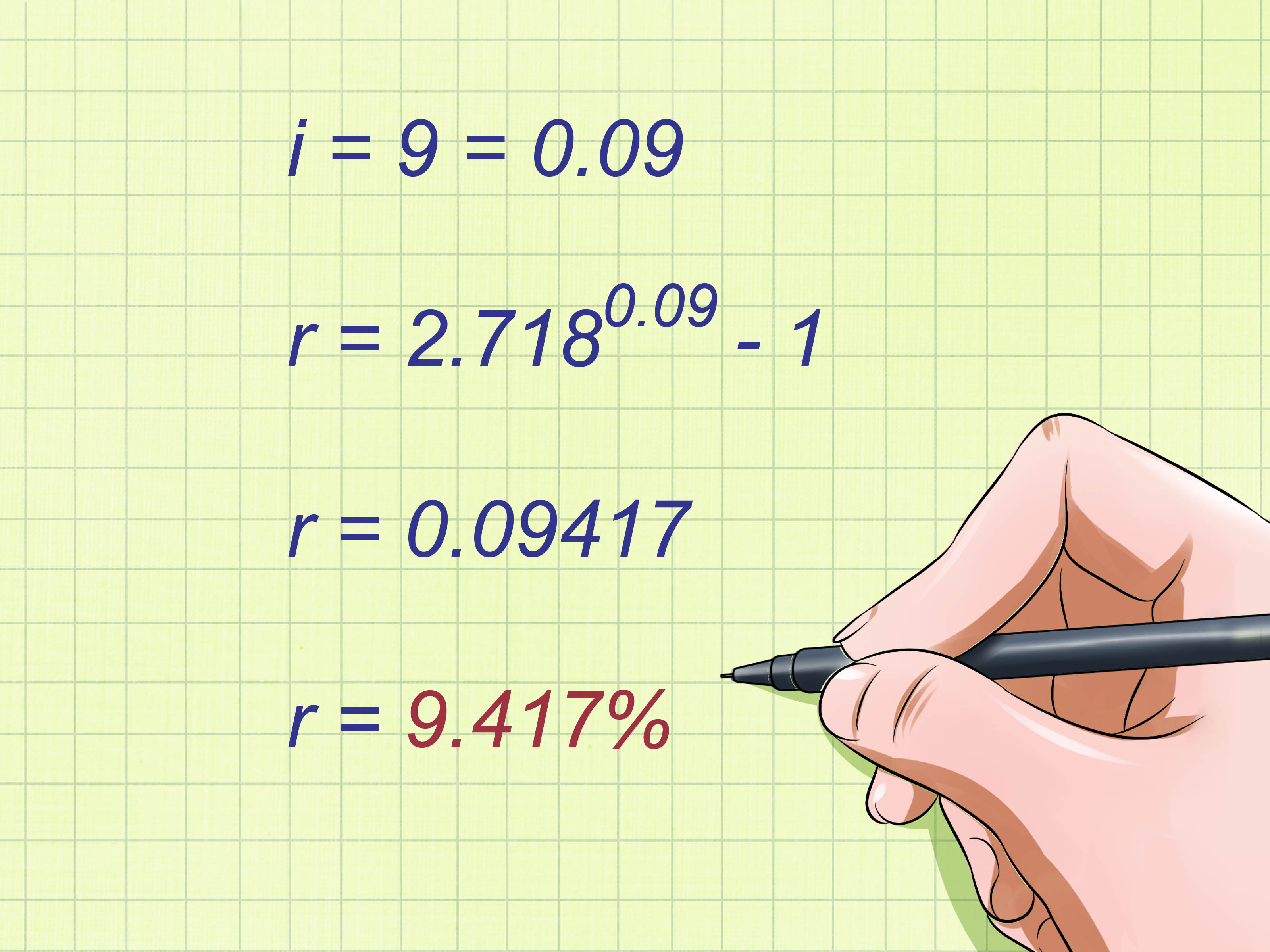
Calculating the effective interest rate (EIR) is a crucial task for anyone involved in finance, whether you're managing personal loans, investments, or business finances. The EIR gives a more accurate view of the actual cost of borrowing or the real rate of return on an investment, accounting for the effects of compounding within a given period. In this blog post, we'll delve into how you can compute the effective interest rate using Microsoft Excel.
What is the Effective Interest Rate?
The Effective Interest Rate (EIR) is the true cost of borrowing or the true return on an investment, considering the effect of compounding over a period. Unlike the nominal interest rate which does not account for compounding, the EIR provides a clearer picture by including the frequency of compounding, making it invaluable for financial planning and decision-making.
Why Use Excel for Computing EIR?
- Simplicity: Excel is user-friendly, allowing even those with basic Excel skills to perform complex calculations.
- Functionality: Excel's built-in functions, like EFFECT and NOMINAL, are specifically designed for financial calculations.
- Automation: Once set up, calculations can be automated for different scenarios or rates, saving time and reducing errors.
Steps to Calculate Effective Interest Rate in Excel
Here's how you can calculate the EIR in Excel:
1. Set Up Your Spreadsheet
- Create headers for the following columns: Nominal Rate, Compounding Frequency, Effective Rate.
2. Enter Known Values
Input your known values:
| Column | Input |
|---|---|
| Nominal Rate | 8% |
| Compounding Frequency | 4 (if quarterly) |
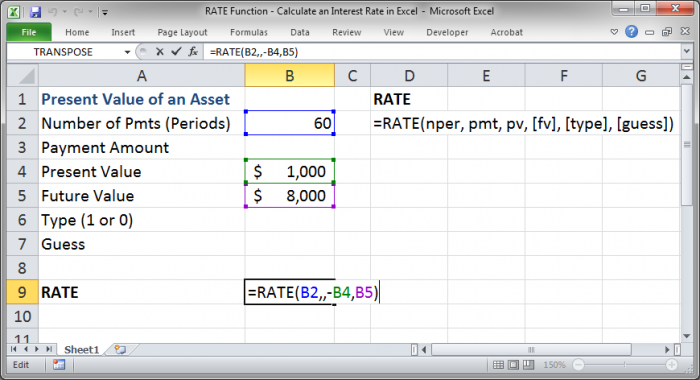
3. Use the EFFECT Function
To calculate the EIR, use the EFFECT function:
=EFFECT(nominal_rate, npery)
Here, nominal_rate is your annual nominal rate (e.g., 8% entered as 0.08), and npery is the number of compounding periods per year (e.g., 4 for quarterly compounding).
4. Enter the Formula
Enter this formula into the Effective Rate cell:
=EFFECT(A2, B2)
Assuming A2 has the nominal rate and B2 has the compounding frequency, you will see the EIR in the cell where you placed the formula.
💡 Note: Ensure your nominal rate is entered as a decimal for accurate calculations.
5. Analyze the Results
Once you have the EIR, you can:
- Compare different loan or investment options with different compounding frequencies.
- Understand the real cost or return better than just using the nominal rate.
What to Do with Your Effective Interest Rate
![[Solved] 12. L023 Compute The Effective Annual Rate Of Interest (A) For 6%... | Course Hero](https://fundraise.jsa.org/assets/img/solved-12-l023-compute-the-effective-annual-rate-of-interest-a-for-6-course-hero.jpeg "[Solved] 12. L023 Compute The Effective Annual Rate Of Interest (A) For 6%... | Course Hero")
Having computed your EIR, here are some practical steps:
- Loan Comparison: Use EIR to compare loans accurately.
- Investment Planning: Determine which investment yields a better return when considering compounding effects.
- Budgeting: Incorporate the effective rate into financial projections or budget planning.
In wrapping up our exploration of computing the Effective Interest Rate in Excel, we've discovered a simple yet powerful tool for financial analysis. From understanding the EIR to using Excel's functions to calculate it, we've covered essential steps to help you make more informed financial decisions. This knowledge equips you with the ability to analyze different financial scenarios accurately, enhancing your financial literacy and planning.
What is the difference between nominal and effective interest rates?
+
The nominal interest rate is the stated rate before accounting for the effects of compounding, whereas the effective interest rate accounts for how often the interest is compounded within a given period, giving a true measure of borrowing cost or investment return.
Can I use Excel for other financial calculations?
+
Yes, Excel is equipped with a wide array of financial functions for various calculations like loan amortization schedules, net present value (NPV), internal rate of return (IRR), and more, making it an essential tool for financial analysis.
How frequently does compounding affect the effective rate?
+
The more frequently interest is compounded, the higher the effective interest rate becomes. For example, monthly compounding will yield a higher EIR than annual compounding for the same nominal rate, as interest earns on interest more frequently.
