5 Ways to Calculate P-Value in Excel Easily
When it comes to statistical analysis, one of the most common and crucial calculations you'll perform is determining the p-value to test the significance of your data. Excel, with its array of statistical functions, is an excellent tool for such calculations. In this post, we will explore five straightforward methods to calculate p-values in Excel, catering to both beginners and advanced users looking to streamline their data analysis process.
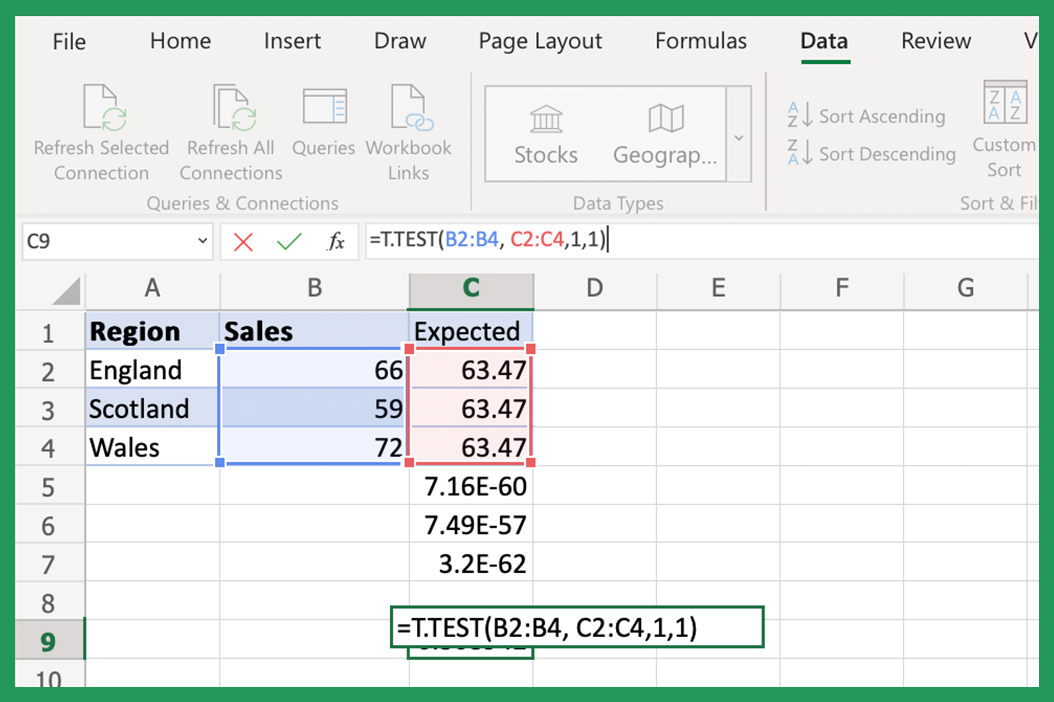
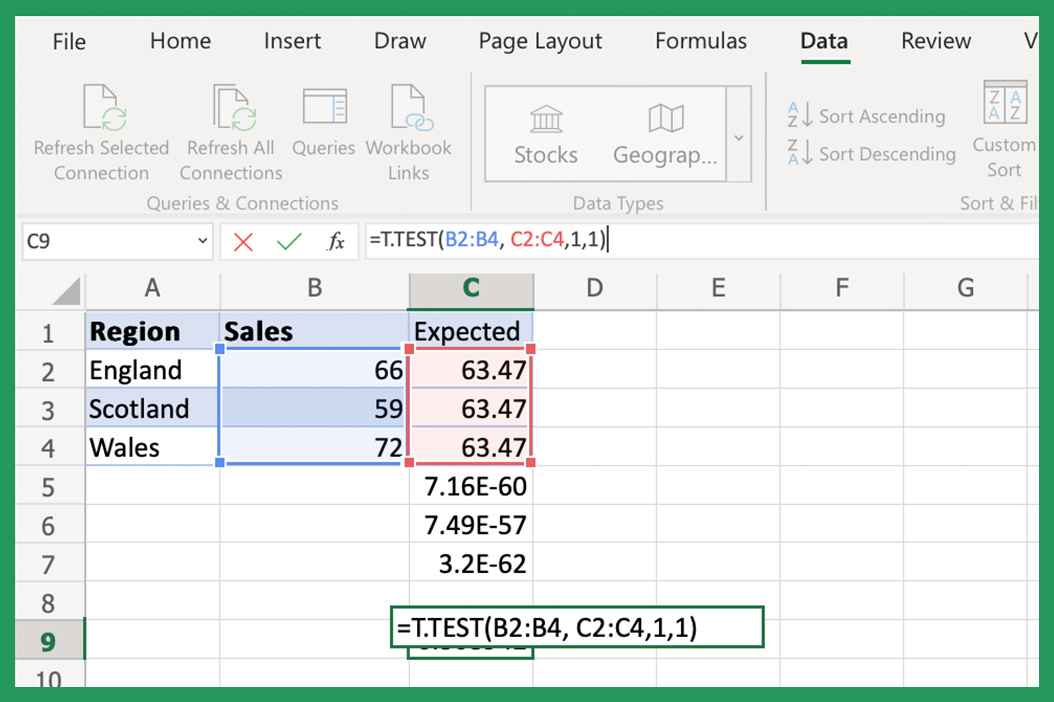
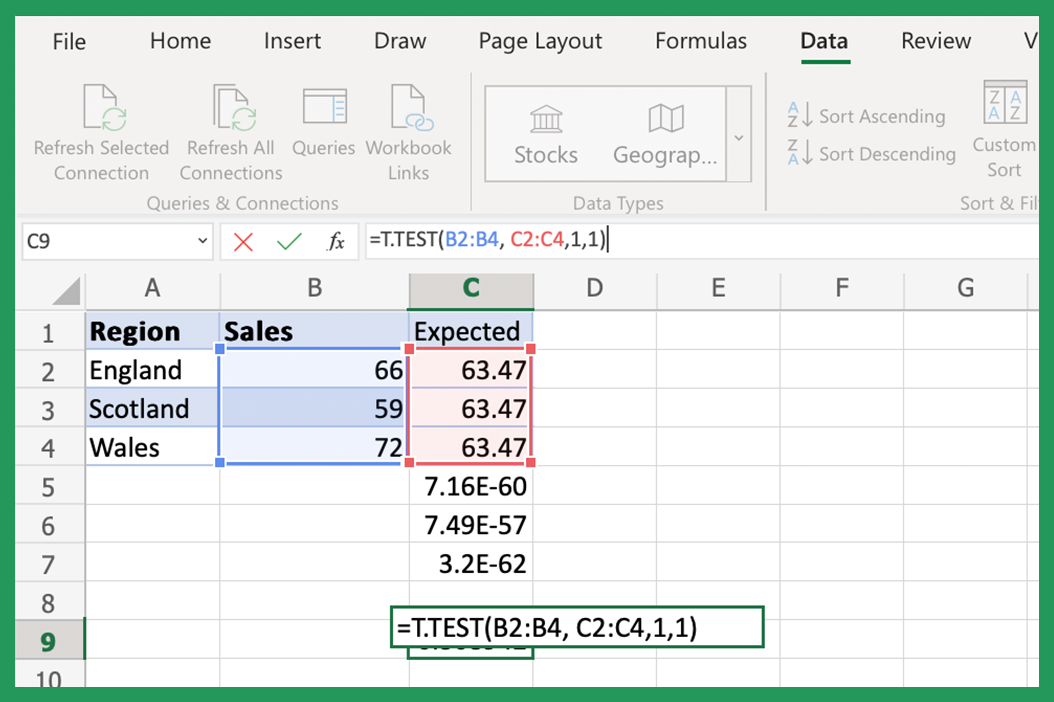
Using the T.TEST Function

The T.TEST function in Excel is designed to provide the p-value for two samples that are assumed to follow the t-distribution. This function is especially useful for conducting hypothesis tests to compare means.
- Function Syntax: T.TEST(array1, array2, tails, type)
- Array1 & Array2: The two data sets you wish to compare.
- Tails: Can be 1 for one-tailed or 2 for two-tailed distribution.
- Type: The type of t-test to be performed, where 1 = paired, 2 = two-sample equal variance (homoscedastic), 3 = two-sample unequal variance (heteroscedastic).
Here's how to use it:
=T.TEST(A2:A10, B2:B10, 2, 2)
This example compares two sets of data, A2:A10 and B2:B10, assuming they are samples from populations with equal variance for a two-tailed test.
📊 Note: Make sure your samples follow the necessary assumptions for the t-test to ensure accurate results.
Using CHITEST or CHISQ.TEST for Chi-Square Tests
For categorical data, a Chi-square test is often used. Here's how you can calculate the p-value using the CHISQ.TEST function:
- Function Syntax: CHISQ.TEST(actual_range, expected_range)
- Actual Range: Observed data set.
- Expected Range: Expected data set based on the null hypothesis.
To perform a Chi-square test:
=CHISQ.TEST(A1:B2, C1:D2)
This function compares the observed frequencies against the expected frequencies in the provided ranges.
📊 Note: CHITEST is an older function; CHISQ.TEST is available in newer versions of Excel.
Using F.TEST for Variance Comparison

The F.TEST function in Excel calculates the p-value for the F-test for comparing variances.
- Function Syntax: F.TEST(array1, array2)
- Array1 & Array2: Two sets of data where you are comparing variances.
Example:
=F.TEST(A2:A20, B2:B20)
This formula gives you the p-value for testing if the variances of the two samples are significantly different.
📊 Note: Use F.TEST when you're interested in variance differences, not mean differences.
Using the NORM.S.INV Function for Normal Distribution
If your data follows a normal distribution, you can use the NORM.S.INV function to find the p-value for a given z-score:
- Function Syntax: NORM.S.INV(z)
- z: The z-score for which you want to find the probability.
Example:
=NORM.S.INV(A2)
Where A2 contains the z-score calculated from your data.
📊 Note: This method requires you to compute the z-score manually or by using other Excel functions like STANDARDIZE.
Custom P-Value Calculation Using Probability Density Functions

For situations where specific Excel functions do not fit, or if you're working with custom distributions or calculations, you can use combinations of Excel's probability density functions:
Consider the following steps:
- Calculate the test statistic (e.g., z-score, t-value, chi-square statistic).
- Use the relevant density function to compute the probability of observing values as extreme or more extreme than your test statistic.
- Double this probability for two-tailed tests.
For example, for a t-test:
=TDIST(ABS(TSTAT), DF, 2)
- TSTAT: The t-statistic calculated from your data.
- DF: Degrees of freedom for the t-distribution.
- 2: Indicates a two-tailed test.
📊 Note: This method gives you more control over the calculation but requires understanding of statistical distributions and formulas.
To wrap up, understanding how to calculate p-values in Excel can significantly enhance your statistical analysis capabilities, allowing for more informed decision-making based on your data. Whether you're conducting a t-test, Chi-square test, comparing variances, dealing with normally distributed data, or crafting a custom solution, Excel offers tools to help you assess the statistical significance of your results. Each method has its unique application, and mastering these techniques will streamline your data analysis process, helping you present and interpret your findings with greater confidence and accuracy.
Can I use Excel for complex statistical analysis?

+
Yes, Excel provides numerous functions for statistical analysis, including regression, ANOVA, and more, but for highly complex analysis, specialized software might be more appropriate.
What is the difference between one-tailed and two-tailed tests?

+
In a one-tailed test, you’re looking for an effect in one direction only, whereas in a two-tailed test, you test for the possibility of an effect in either direction.
How do I interpret the p-value?
+
A p-value less than your chosen significance level (commonly 0.05) indicates that the observed effect is statistically significant, suggesting the results are not due to random chance alone.
Are there limitations to using Excel for statistical analysis?
+
Excel has limitations in terms of precision, especially with very large datasets, and it lacks some advanced statistical methods available in dedicated statistical software.