5 Easy Steps to Calculate Z Scores in Excel
The application of statistical tools in data analysis is indispensable for analysts, researchers, and students aiming to understand and interpret data effectively. One of the key statistics often used in this process is the Z score, which measures how far a particular data point deviates from the mean of a dataset in terms of standard deviation. Calculating Z scores can be straightforward, particularly if you're using tools like Microsoft Excel. Here's how you can calculate Z scores in just five easy steps.
Step 1: Prepare Your Data
First and foremost, ensure that your data is well-organized. In Excel:
- Enter your dataset into a column or row.
- Ensure there are no missing values or errors in your dataset as these could skew your results.
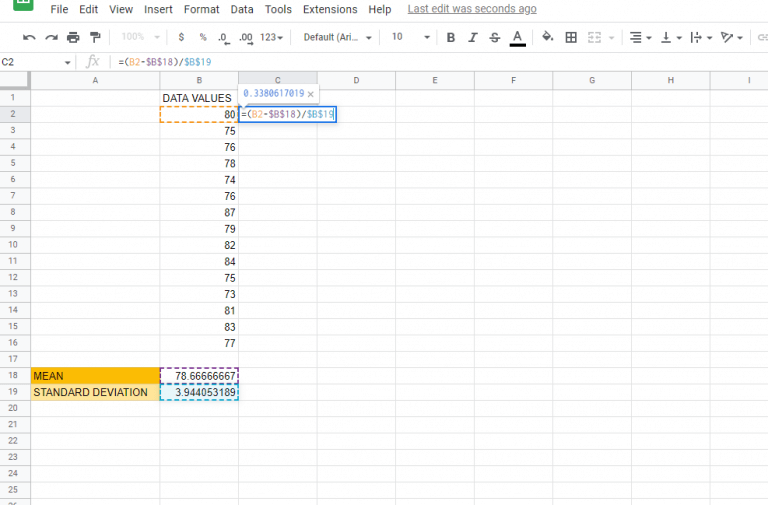
Step 2: Calculate the Mean
The Z score calculation requires the mean (average) of your dataset. Here’s how to calculate it:
- Select an empty cell where you want the mean to appear.
- Use the AVERAGE function:
=AVERAGE(A1:A100), assuming your data spans from A1 to A100. Adjust the range according to your dataset.
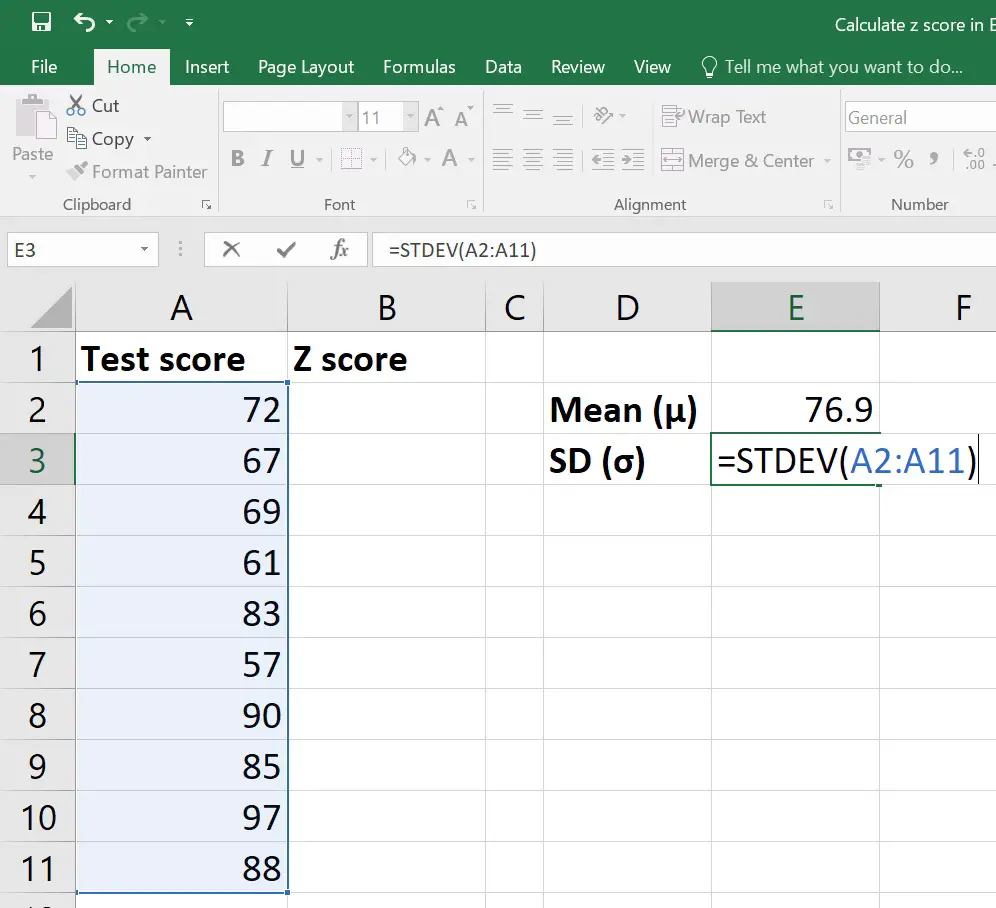
Step 3: Compute the Standard Deviation

After finding the mean, the next step is to calculate the standard deviation:
- Again, choose an empty cell for the result.
- Enter the STDEV.P or STDEV.S function, depending on whether you’re dealing with the entire population or a sample:
- For a sample:
=STDEV.S(A1:A100) - For the entire population:
=STDEV.P(A1:A100)
- For a sample:
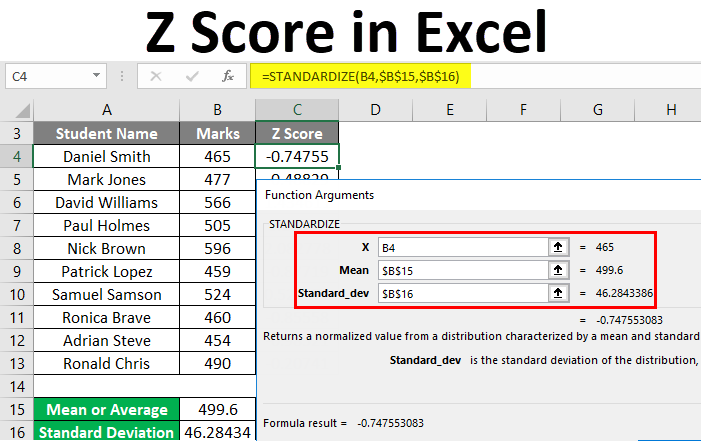
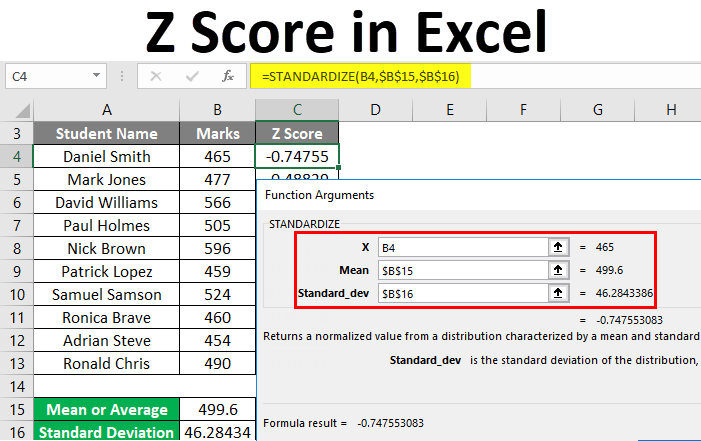
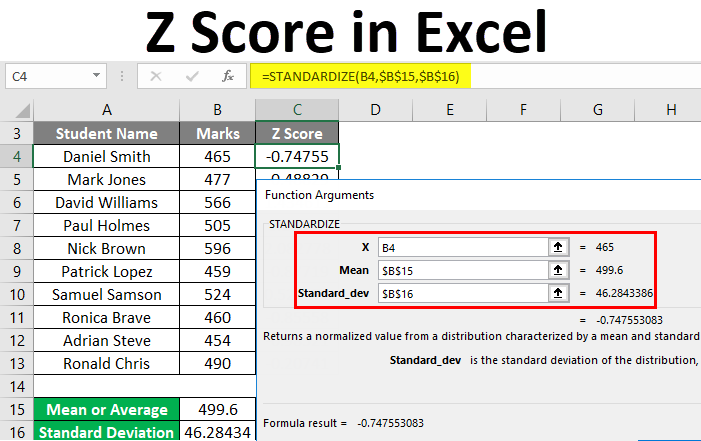
Step 4: Calculate the Z Score
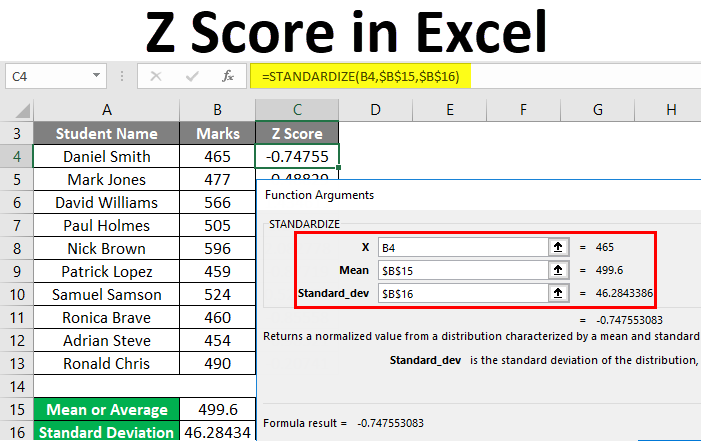
With the mean and standard deviation at hand, calculating the Z score is straightforward:
- Select another empty cell where you wish to display the Z score.
- Use the formula:
=Z=(A1-Mean)/STDDEV, where:A1is the data point for which you’re calculating the Z score.Meanis the cell containing the mean.STDDEVis the cell with the standard deviation.
Repeat this calculation for each data point if you need multiple Z scores.
📘 Note: When using this formula, ensure that the cell references for Mean and STDDEV are absolute by adding the </code> sign, like this: <code>A1</code> and <code>A$2, to lock them in place during copying.
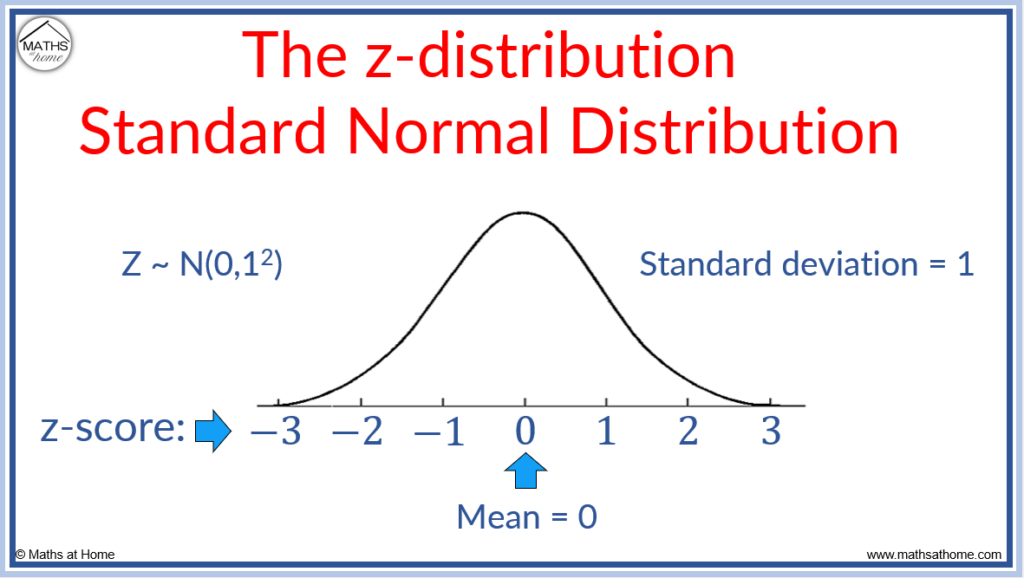
Step 5: Interpret Your Z Scores
Understanding what Z scores mean:
- A Z score of 0 indicates the data point is exactly at the mean.
- Positive Z scores signify that the data point is above the mean.
- Negative Z scores indicate the data point falls below the mean.
- The further the Z score is from zero, the more extreme the data point is within your dataset.
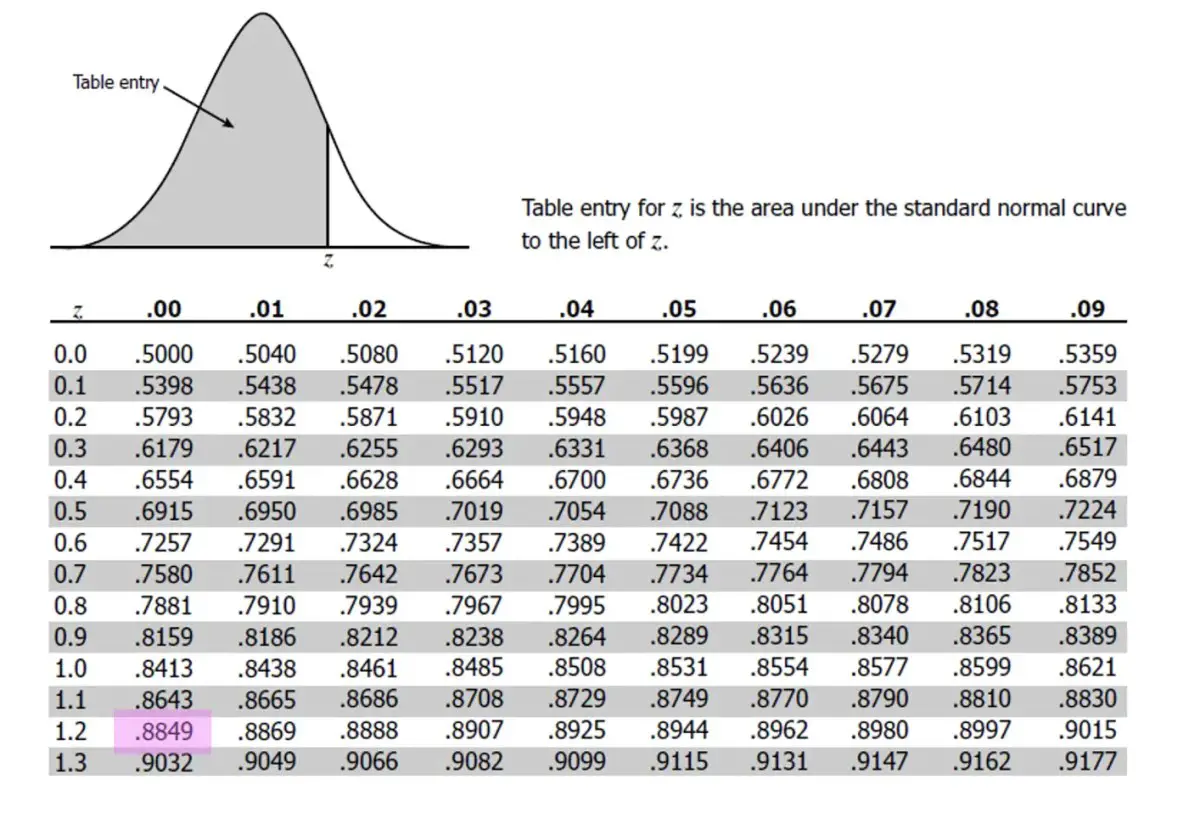
Here's a table to illustrate different Z scores and their implications:
| Z Score | Interpretation |
|---|---|
| 2.0 | The data point is 2 standard deviations above the mean. |
| 0.0 | The data point is equal to the mean. |
| -1.5 | The data point is 1.5 standard deviations below the mean. |
In conclusion, Z scores are a powerful tool for understanding the relative position of data points within a dataset. With Excel, the process is simplified to just five steps: prepare your data, calculate the mean, find the standard deviation, compute Z scores, and then interpret them. By following these steps, you can conduct more nuanced data analysis, making it easier to identify outliers, understand distribution, and make data-driven decisions. Keep in mind, these calculations are fundamental, and they form the groundwork for more complex statistical analyses.
Can I calculate Z scores for a skewed distribution?
+
Yes, but keep in mind that Z scores assume your data follows a normal distribution. For significantly skewed data, consider using other normalization techniques or distribution-specific methods.
What should I do if I have missing data points?
+
Handle missing data points carefully. You can either exclude these points from your calculation or impute values, depending on your dataset’s nature and the analysis’s purpose.
How does the sample vs. population affect Z score calculation?
+
The difference lies in how standard deviation is calculated. Use STDEV.S for a sample and STDEV.P for the population. The formula for the Z score itself doesn’t change, but the standard deviation impacts the Z score.