5 Easy Steps to Calculate Median Absolute Deviation in Excel
Introduction to Median Absolute Deviation (MAD)
When it comes to statistics, understanding the variability within a dataset is crucial. One of the lesser-known yet highly useful metrics for this is the Median Absolute Deviation (MAD). MAD provides a robust measure of the spread of the data, which is less influenced by outliers compared to other measures like the standard deviation. In this post, we’ll walk through five easy steps to calculate MAD in Excel, ensuring you can quickly and accurately assess the dispersion in your data.

Step 1: Organize Your Data

Before you can dive into calculations, your data needs to be properly organized:
- Open Microsoft Excel and enter your dataset in one column.
- Ensure there are no blank cells in your data series, as Excel might skip over these when performing calculations.
This preliminary step ensures that your subsequent calculations are accurate and efficient.

Step 2: Calculate the Median of the Dataset
To compute MAD, we first need to find the median:
- Go to an empty cell, type in
=MEDIAN(A2:A10)assuming your data is in column A from row 2 to 10. - Press Enter. Excel will now display the median value.
The median represents the middle value of your dataset and serves as the baseline for calculating deviations.

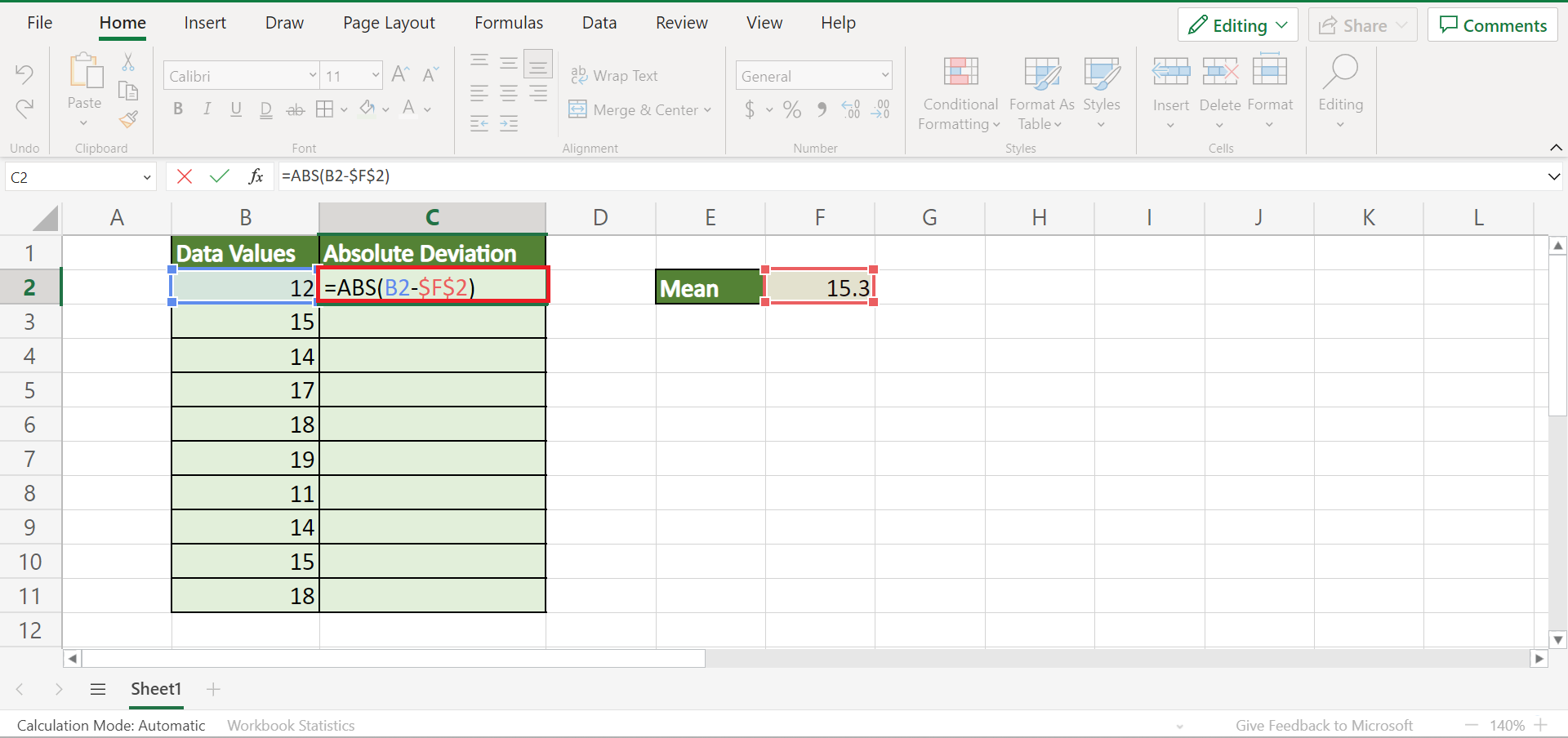
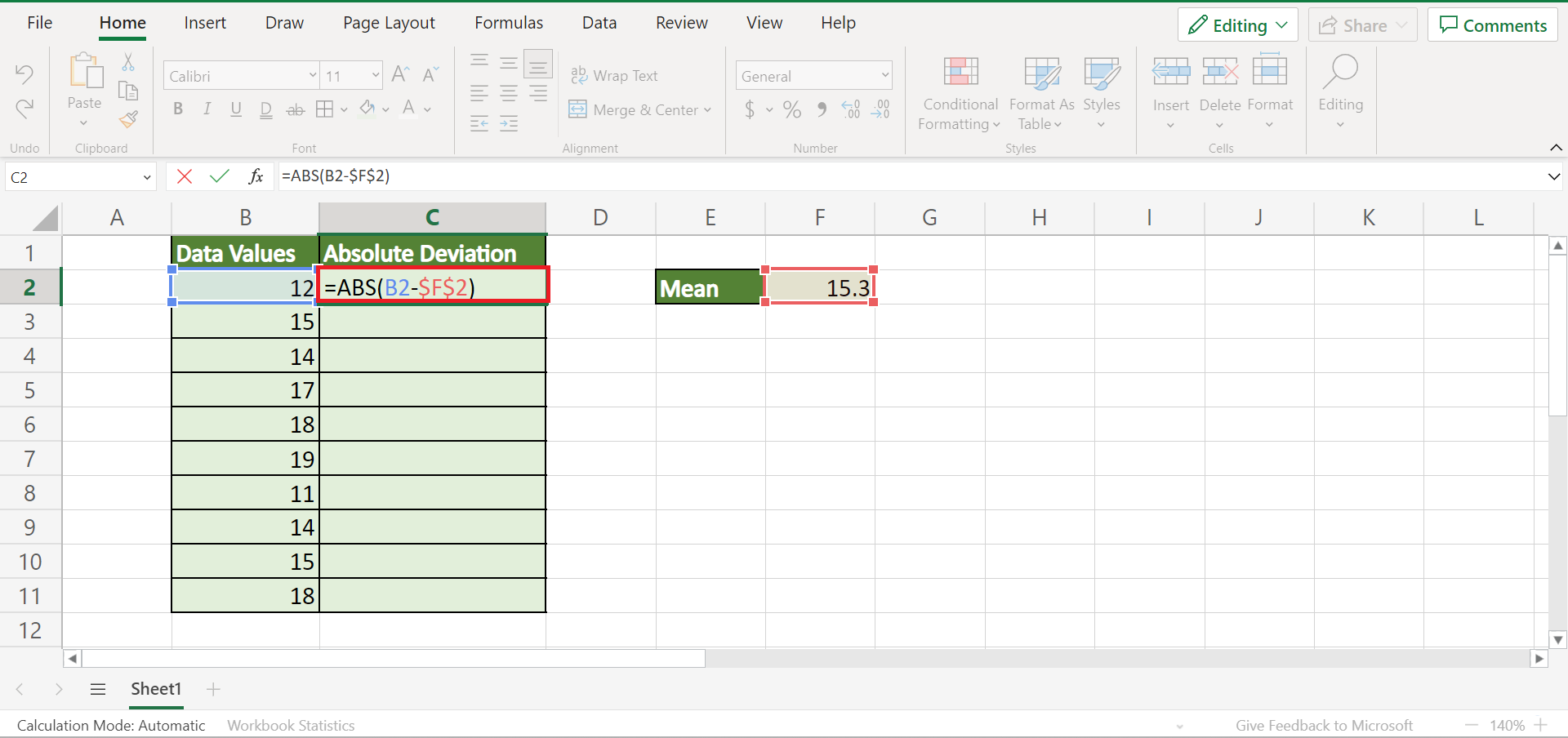
Step 3: Compute the Absolute Deviations
Now, calculate the absolute difference between each data point and the median:
- In an adjacent column, use the formula
=ABS(A2 - [Median Value]). If your median is in cell B2, this would be=ABS(A2 - $B$2). - Drag this formula down to apply it to all your data points.
This step quantifies the spread of each data point from the median.
| Data | Absolute Deviation |
|---|---|
| 10 | =ABS(A2 - B2) |
| 20 | =ABS(A3 - B2) |

🌟 Note: Ensure the dollar signs ($) are used to create an absolute reference to the cell containing the median value.
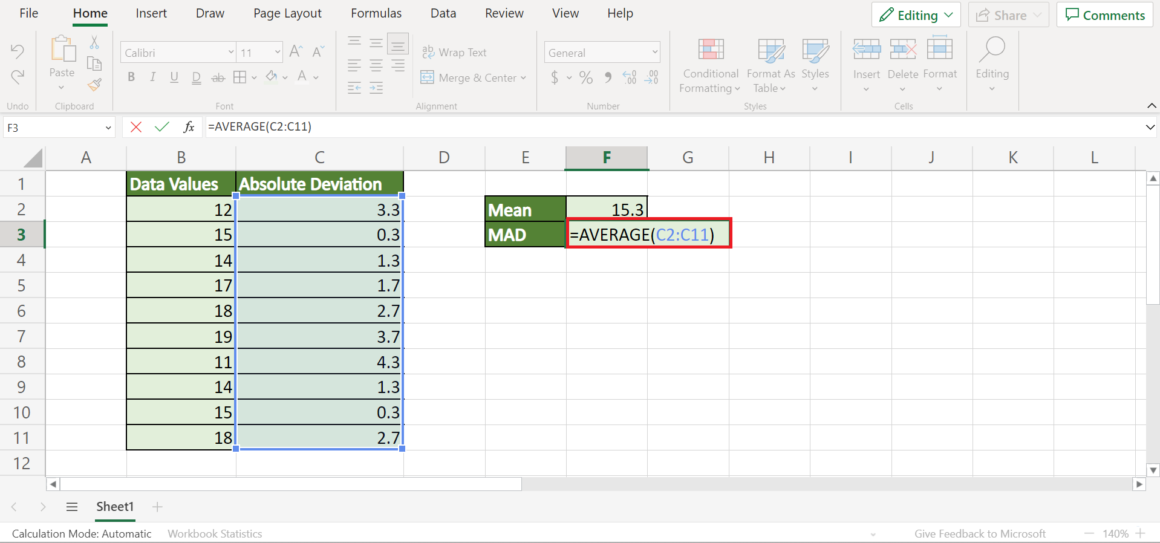
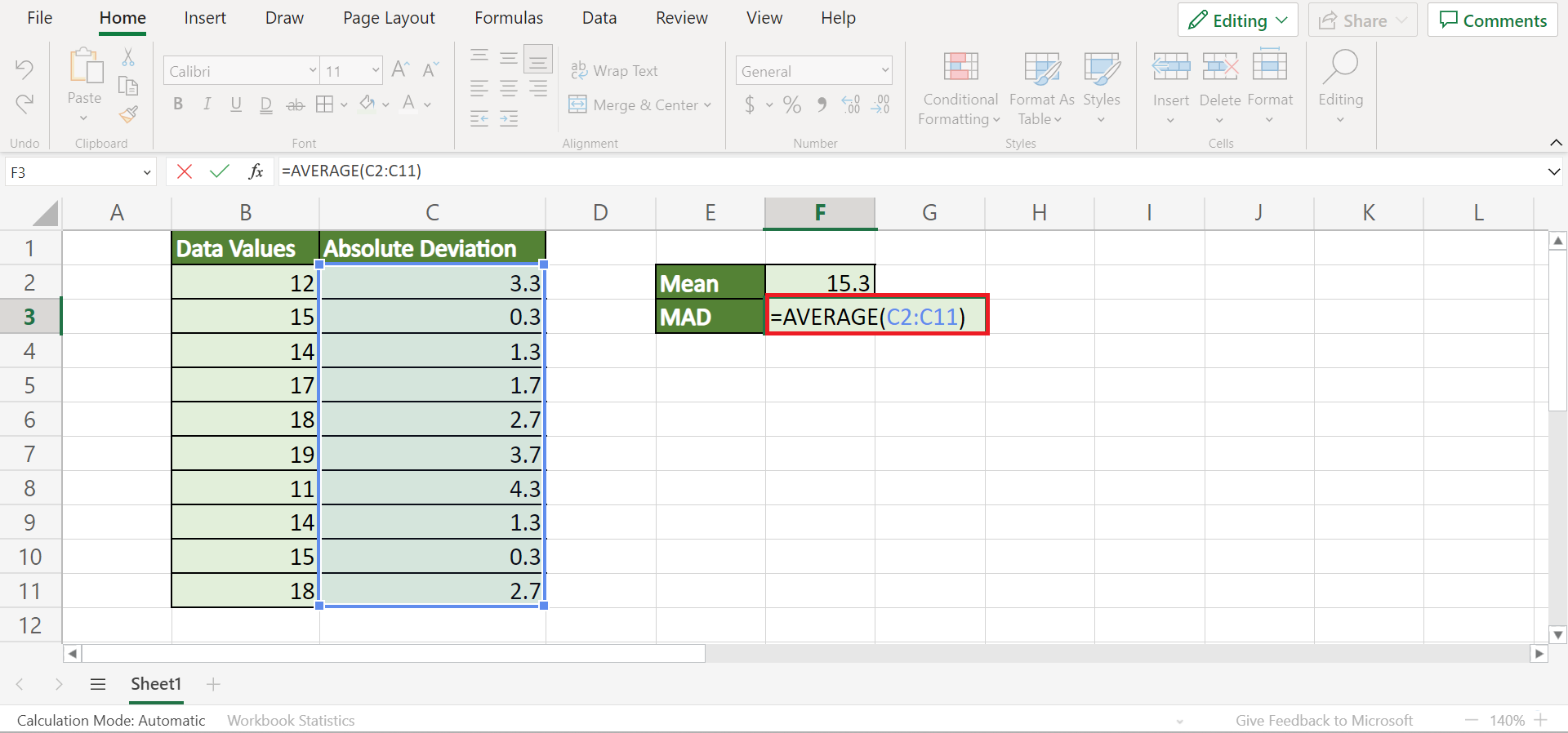
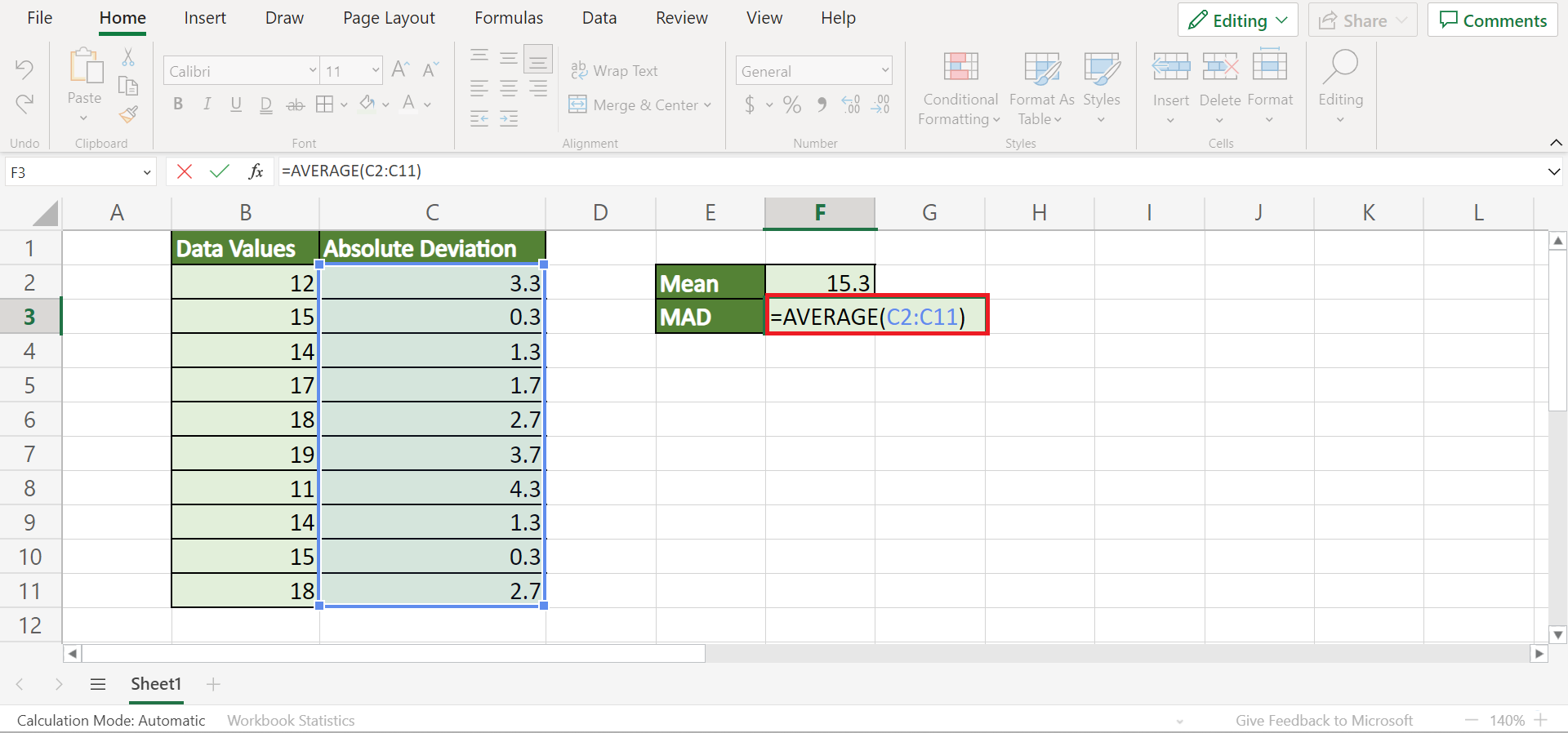
Step 4: Determine the Median of the Absolute Deviations

Next, we find the median of these absolute deviations:
- Select an empty cell, type
=MEDIAN([Range of Absolute Deviations])to get the median absolute deviation.
This value, known as MAD, provides a measure of variability:

Step 5: Analyze and Interpret the Results
After calculating MAD:
- Review the MAD value to understand the spread in your data.
- Lower MAD indicates less variability, whereas a higher MAD suggests greater dispersion.
- Consider the context and domain-specific factors when interpreting the results.
In this guide, we've covered the essentials of calculating Median Absolute Deviation in Excel, providing a robust tool for understanding data variability. Here's a recap:
Organize your data in Excel to ensure accurate calculations.
Find the median of your dataset to set the baseline for deviations.
Compute the absolute deviations of each data point from the median.
Determine the median of these deviations, which is your MAD.
Use MAD to gain insights into data dispersion, mindful of context and domain relevance.
Remember, while this is a basic calculation, Excel's flexibility allows for further analysis, data visualization, and integration with other statistical tools or packages.
Why use Median Absolute Deviation (MAD) instead of Standard Deviation?
+
MAD is more resistant to outliers and non-normal distributions, providing a more stable measure of spread in various data scenarios.
Can I use this method for non-numerical data?
+
This method is designed for numerical data. For non-numerical data, other techniques like mode or frequency analysis might be more appropriate.
What if my dataset has an even number of values?
+
Excel calculates the median as the average of the two middle numbers. Ensure to sort your data first for accurate results.