How To Find Critical Value In Excel
When working with statistical data, understanding how to calculate and interpret various statistical measures is crucial, especially for research, business analysis, or educational purposes. One of these key statistical metrics is the critical value. This post will guide you through the process of finding critical values using Microsoft Excel, making it easier for you to perform statistical analysis without needing advanced statistical software.
Understanding Critical Values

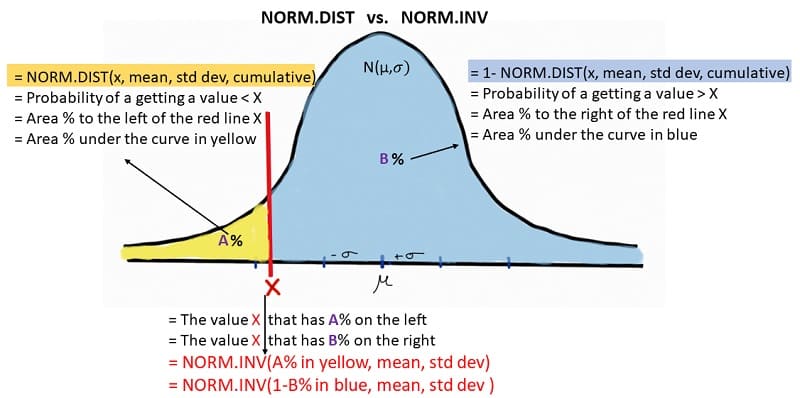
Before diving into Excel, let’s clarify what a critical value is. In statistics, a critical value is a cut-off value that defines the boundaries beyond which we reject the null hypothesis in hypothesis testing. These values depend on the significance level (commonly denoted as alpha, α), the type of test, and the distribution (normal, t-distribution, chi-square, etc.).
Tools You’ll Need
- A computer with Microsoft Excel installed (Excel 2013 or later).
- A basic understanding of statistical concepts like significance level, p-value, and test statistics.
Finding Critical Values in Excel

For Normal Distribution
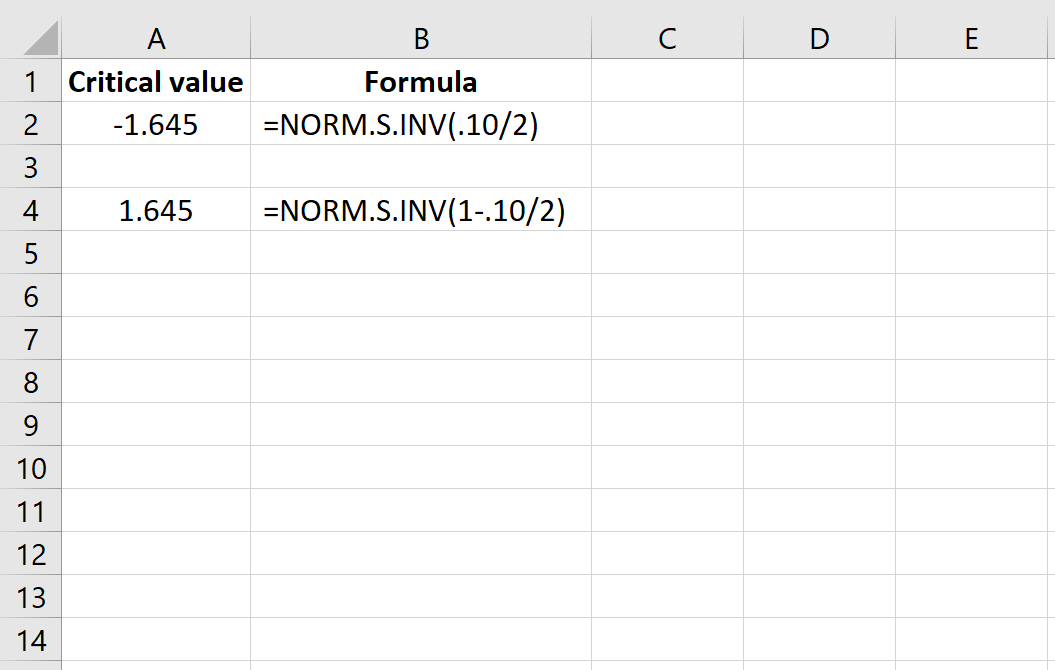
Excel provides several functions for working with normal distribution:
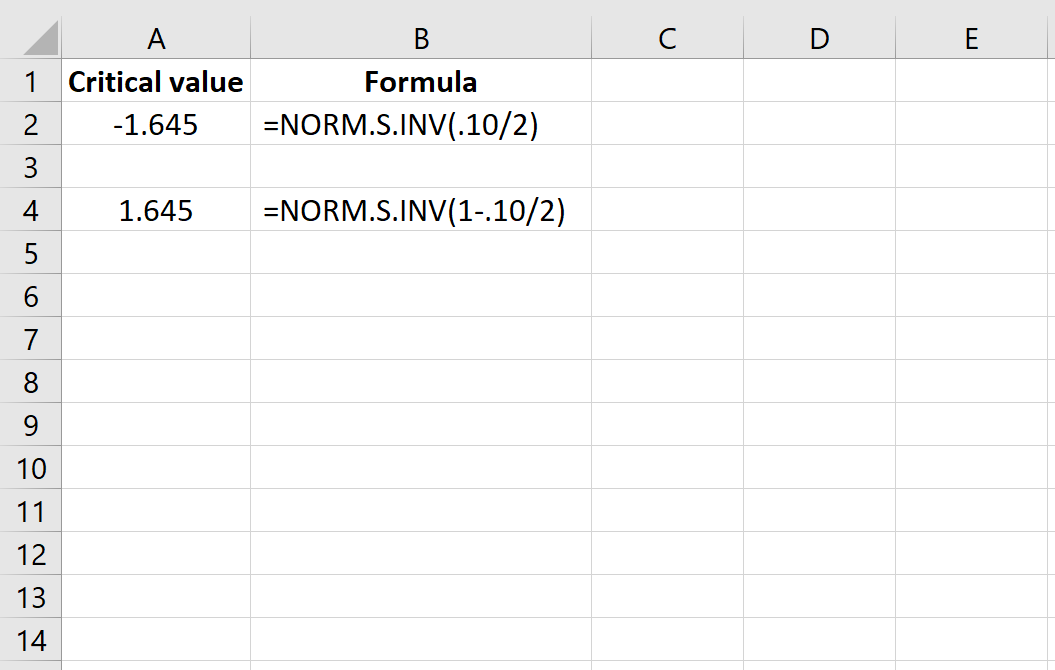
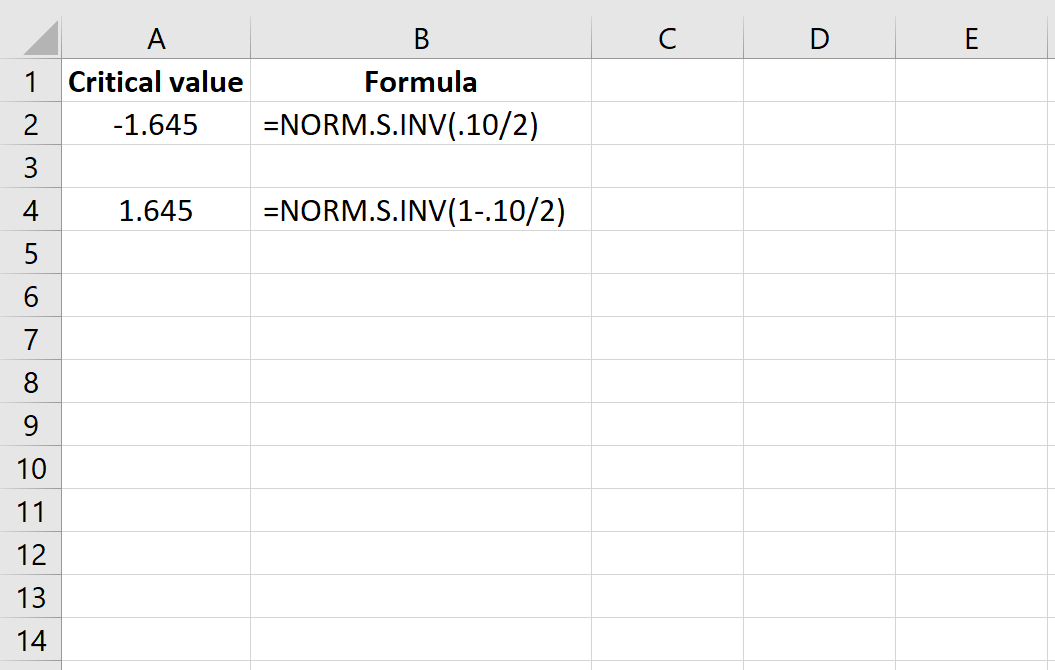
- NORM.S.INV(p): This function returns the inverse of the standard normal cumulative distribution, which gives you the z-score for a given significance level (p).
Here's how to find a critical value for a two-tailed test:
| Step | Action |
|---|---|
| 1 | Determine your alpha level. For example, if you want a 95% confidence interval, α = 0.05. |
| 2 | Since it's a two-tailed test, split alpha: α/2 = 0.025. |
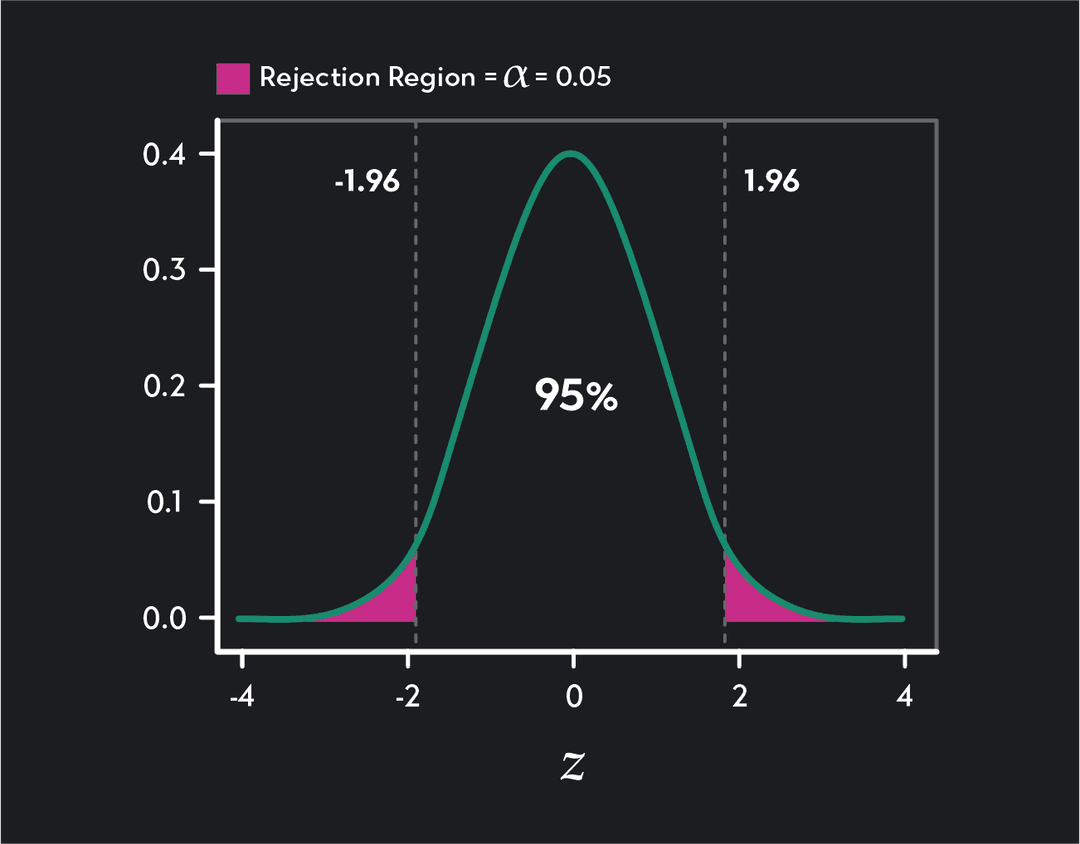
| 3 | Use the formula =NORM.S.INV(1-0.025) to find the z-value. This formula calculates the value from the right tail. |
🔍 Note: Remember that for a one-tailed test, you would use the full alpha value directly in the function.
For T-Distribution

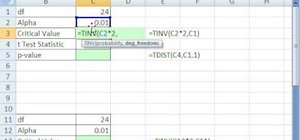
If you’re dealing with small sample sizes, you’ll use the t-distribution. Here’s how to find the critical value for t-distribution:
- T.INV(p,deg_freedom) for one-tailed tests.
- T.INV.2T(p,deg_freedom) for two-tailed tests.
| Step | Action |
|---|---|
| 1 | Determine degrees of freedom (df). For example, if your sample size is 25, df = 24. |
| 2 | Choose alpha. For example, if α = 0.05, use T.INV.2T(0.05, 24). |
| 3 | Execute the formula in Excel to get your critical t-value. |
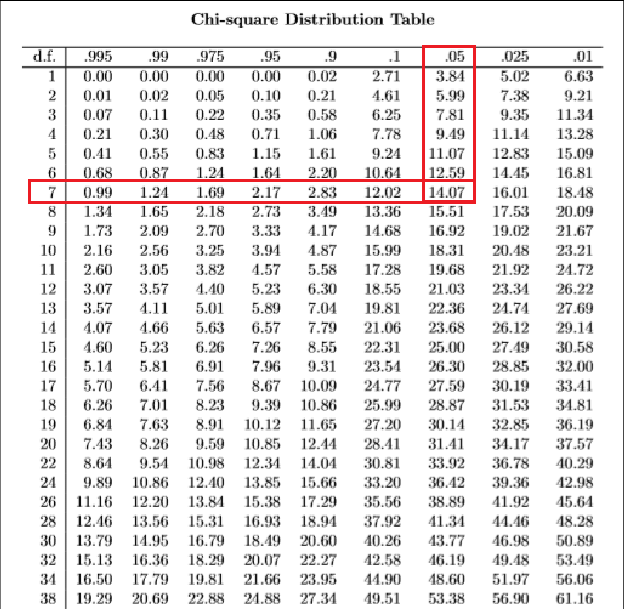
For Chi-Square Distribution
Chi-square distribution is used for tests involving categorical data or when dealing with variance. Excel’s function for this is:
- CHI.INV(p,deg_freedom) or CHI.INV.RT(p,deg_freedom) for the right-tailed test.
Key Points to Remember
- Significance Level (α): This is the probability of rejecting the null hypothesis when it is true.
- Tails: One or two-tailed tests influence how you use the critical value functions.
- Distribution: Choose the appropriate distribution based on your data’s properties or the type of test.
Understanding and correctly finding critical values in Excel enhances your ability to perform accurate hypothesis testing, thus helping in making more reliable conclusions from your data.
Factors Affecting Critical Values

Critical values are influenced by several factors:
- Sample Size: Larger samples decrease the critical value due to increased statistical power.
- Distribution: Different distributions will yield different critical values even with the same α.
- Test Type: Whether you are conducting one-tailed or two-tailed tests affects the calculation.
- Level of Significance (α): Decreasing α increases the critical value, making it harder to reject the null hypothesis.
When conducting hypothesis tests, always ensure you:
- Check if your data meets the assumptions of the test.
- Use the correct distribution for your test.
- Understand the context in which the test is being applied.
In summary, Excel offers an accessible way to find critical values for various statistical tests. By following the steps outlined, you can calculate these values for normal, t, and chi-square distributions, making hypothesis testing a less daunting task. Remember that while Excel simplifies these calculations, understanding the underlying statistical principles is vital for accurate interpretation of results.
Why do I need to find critical values in Excel?
+
Critical values help in hypothesis testing by defining the thresholds for rejecting or accepting the null hypothesis based on statistical evidence.
Can I find critical values for any distribution in Excel?
+
Excel provides functions for common distributions like normal, t, and chi-square, but not for all. For less common distributions, you might need specialized software or advanced Excel skills.
What if my data doesn’t meet the assumptions for these tests?
+
If your data does not meet the assumptions of parametric tests, consider non-parametric alternatives or explore data transformation techniques.