Effortlessly Calculate MSE in Excel - Quick Guide
Welcome to this comprehensive guide on how to effortlessly calculate Mean Squared Error (MSE) using Microsoft Excel. Whether you're a student, researcher, or data analyst, understanding how to measure the quality of your predictions or regression models can be crucial. In this tutorial, we'll go through each step to ensure you can compute MSE with ease.
What is Mean Squared Error (MSE)?
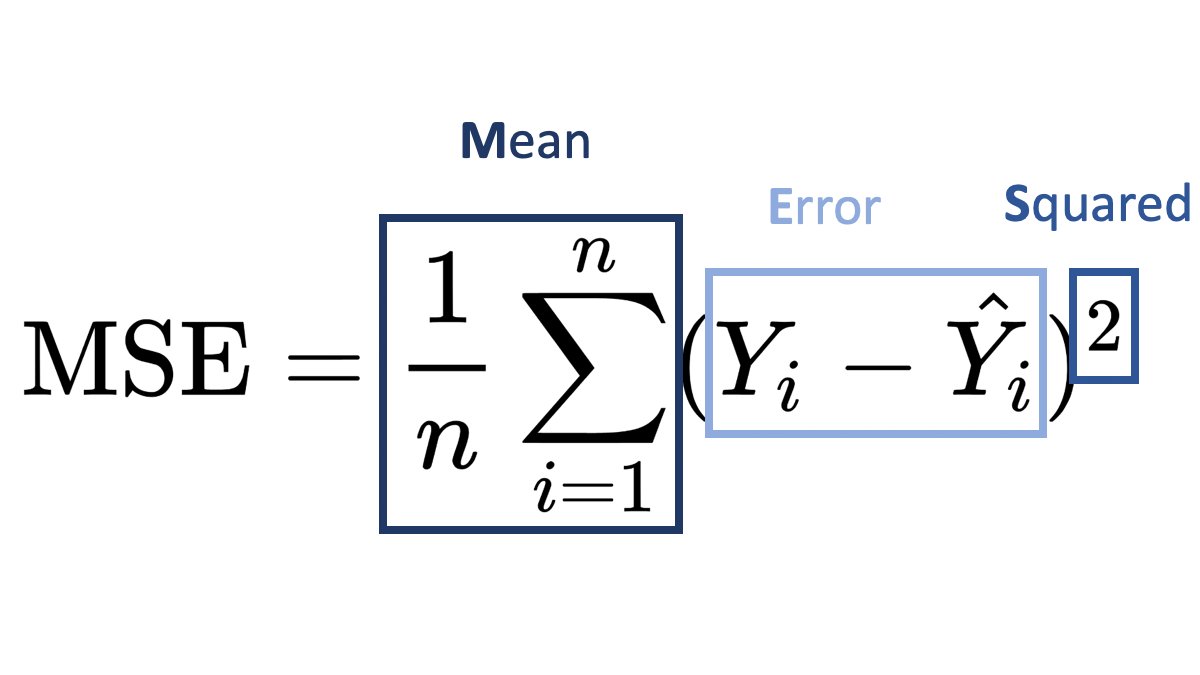
Mean Squared Error is a statistical metric used to assess the average squared difference between the predicted values and the actual values. Here’s how it’s calculated:
- Formula: MSE = (1/n) * Σ(actual_value - predicted_value)² where n is the number of data points.
- Application: MSE is often used in regression analysis to gauge how well a model fits the data, lower values indicating a better fit.
Step-by-Step Guide to Calculate MSE in Excel
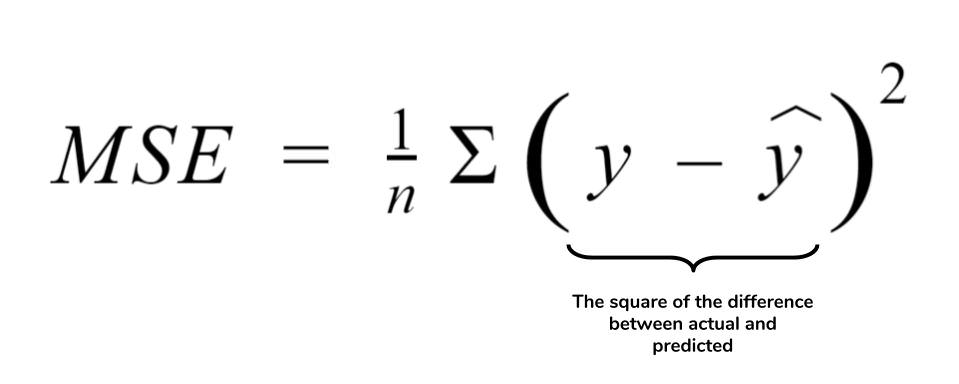
Let’s break down the process into simple steps:
Step 1: Data Preparation

Before you calculate MSE, make sure your data is ready:
- Enter your actual values in one column (say Column A).
- Enter your predicted values in another column (say Column B).
- Ensure both columns are of the same length.
Step 2: Squaring the Difference

Now, we’ll create a third column to calculate the squared difference between actual and predicted values:
- In Column C, type the formula
=POWER(A2-B2, 2)in the second row (assuming the first row is for column headers). - Drag this formula down to fill the column corresponding to your data set.
🔍 Note: Using the POWER function ensures you get the exact squared difference. Also, remember to adjust cell references according to your data placement.
Step 3: Summing Up the Squared Differences
Next, you need to sum all the squared differences:
- In a new cell, for example, F1, type
=SUM(C2:C[n])where n is the last row with data.
Step 4: Counting the Number of Observations

To calculate MSE, we need the count of data points:
- In cell F2, type
=COUNTA(A2:A[n])or you could manually enter the number if you know it.
Step 5: Calculating the MSE
Now, apply the MSE formula:
- In cell F3, enter the formula
=F1/F2which divides the sum of squared differences by the count of data points.
| Data Point | Actual Value | Predicted Value | Difference Squared |
|---|---|---|---|
| 1 | 2.5 | 2.7 | 0.04 |
| 2 | 3.0 | 3.1 | 0.01 |
| 3 | 4.2 | 4.5 | 0.09 |

Step 6: Verifying the Calculation
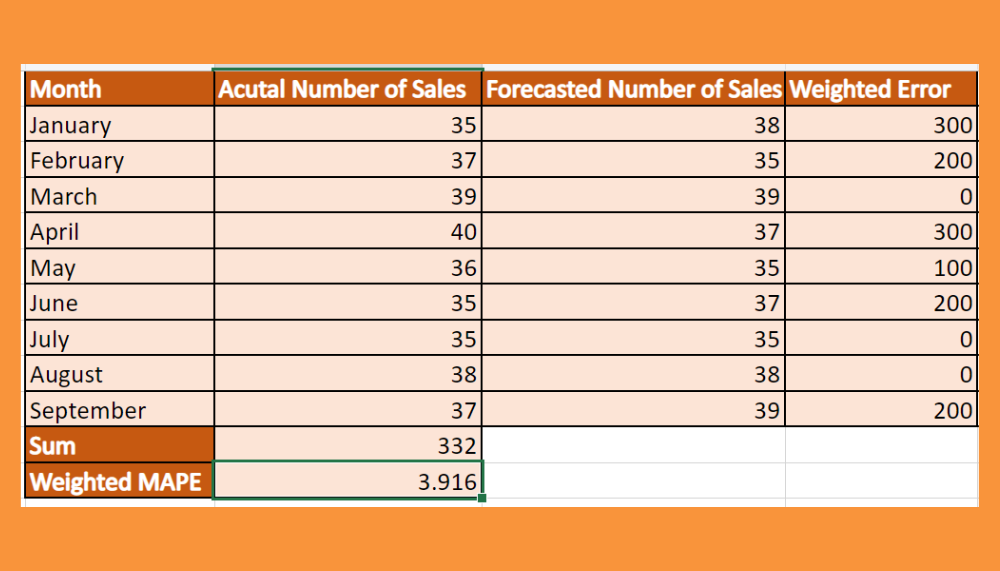
If you want to verify your MSE:
- Check if the sum in F1 matches your manual sum or calculator's sum of the squared differences.
- Divide that sum by the count of data points to confirm the MSE value.
📈 Note: To ensure the accuracy of your calculations, always double-check your MSE with manual computation or another tool like Python or R if available.
When to Use MSE?

MSE is particularly useful in:
- Regression Analysis: To assess how well a model is predicting continuous outcomes.
- Model Comparison: When you're choosing between different models, MSE can help identify the one with the best predictive power.
Now that you've learned how to calculate MSE in Excel, let's wrap up this guide with a recap:
The journey through calculating Mean Squared Error in Excel has shown you how to:
- Prepare your data accurately for MSE calculation.
- Use formulas to compute the squared differences and then aggregate them.
- Interpret the results to understand the performance of your predictions or models.
The steps provided here are not only straightforward but also offer a solid foundation for further statistical analysis in Excel. While MSE is an invaluable tool, remember that different scenarios might require different error metrics. Keep exploring, practicing, and refining your analytical skills to get the most out of your data analysis!
Why is MSE important in regression analysis?
+
MSE provides a measure of how well a regression model predicts the dependent variable by giving the average squared difference between observed and predicted outcomes.
Can MSE be negative?

+
No, MSE cannot be negative because you’re squaring the differences, which always yields a non-negative number.
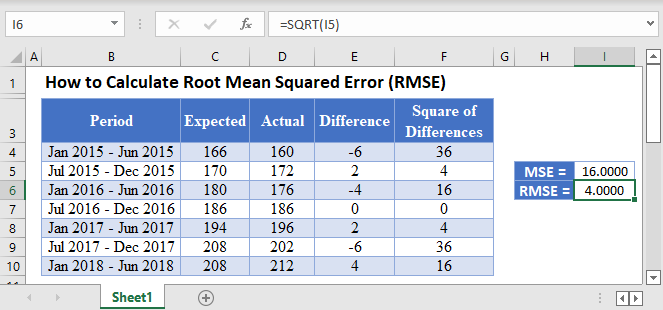
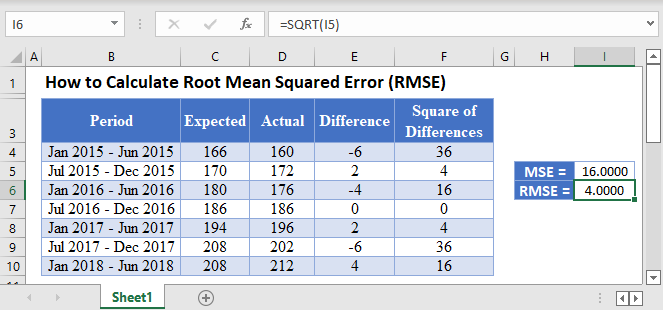
How does MSE relate to Root Mean Squared Error (RMSE)?

+
RMSE is simply the square root of MSE, providing an error measure in the same units as the original data for better interpretability.