Easily Calculate P-Value in Excel: Quick Guide
In the realm of statistical analysis, understanding how to derive and interpret key statistical measures can significantly enhance your ability to draw meaningful conclusions from data. One such measure, the p-value, is crucial for hypothesis testing, where it helps determine the significance of results. If you're working with datasets in Excel, knowing how to calculate the p-value can provide insights into your data's statistical significance. Here's a step-by-step guide on how to calculate the p-value in Excel efficiently.
Understanding the P-Value

Before diving into the calculation, let’s understand what a p-value represents. The p-value, or probability value, indicates the likelihood that the observed data could have occurred by random chance if the null hypothesis is true. A low p-value (typically less than 0.05) suggests that the observed data are unlikely to have occurred by chance, leading to the rejection of the null hypothesis. Here’s what you need to know:
- Null Hypothesis (H0): The statement of no effect or no difference.
- Alternative Hypothesis (H1): A statement that contradicts the null hypothesis.
- Significance Level (α): Often set at 0.05, this is the threshold for deciding whether to reject H0.
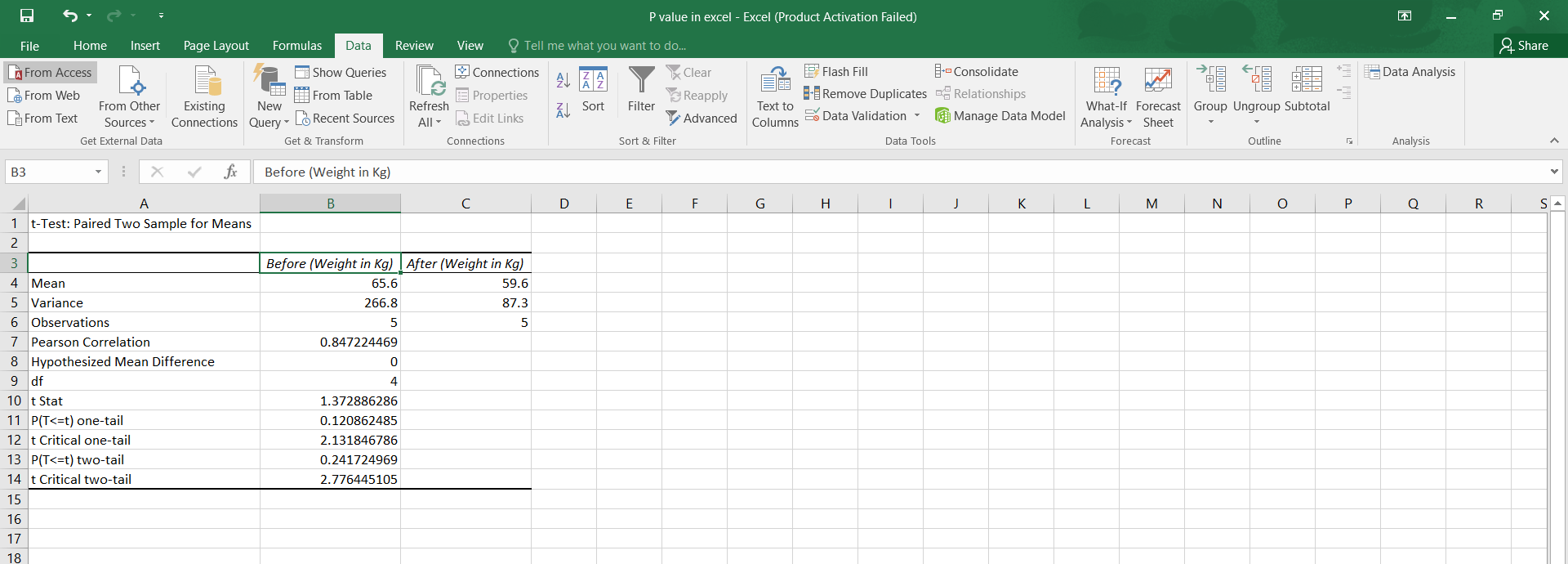
Calculating the P-Value with T-TEST

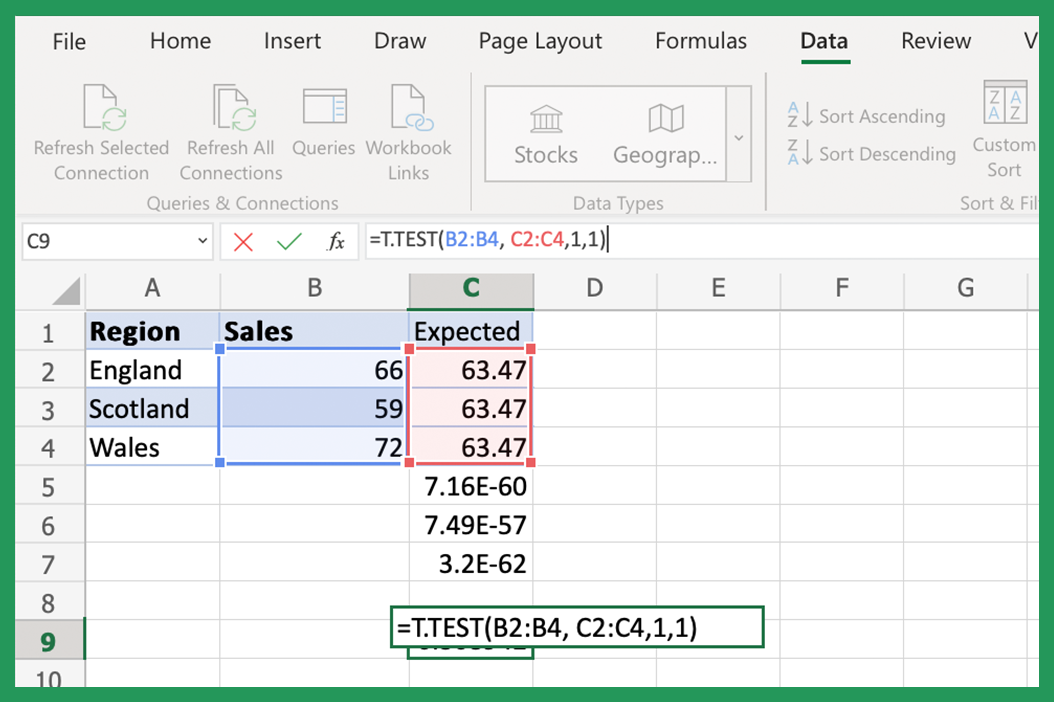
Excel offers a straightforward function for performing a t-test to calculate the p-value:
- Select a cell where you want the result to appear.
- Go to the Formula tab.
- Type =T.TEST(array1, array2, tails, type) in the formula bar.
| Argument | Description |
|---|---|
| array1 | Your first data set |
| array2 | Your second data set for comparison |
| tails | Set to 1 for one-tailed or 2 for two-tailed test |
| type | Set to 1 for paired, 2 for two-sample equal variance, 3 for two-sample unequal variance |

Alternative Methods

Besides the t-test, other functions in Excel can also be used to calculate p-values:
CHI-SQUARE Test

The CHISQ.TEST or CHISQ.DIST functions can be employed for categorical data analysis:
- CHISQ.TEST(actual_range, expected_range) provides the p-value directly.
- CHISQ.DIST(x, deg_freedom, cumulative) calculates cumulative distribution, requiring additional steps for p-value.
🧐 Note: Ensure your data fits the Chi-square test's assumption for observed and expected frequencies.
Interpreting the Results

Once you’ve calculated the p-value, here’s how to interpret it:
- If p-value ≤ α: Reject the null hypothesis. There is statistical evidence to support your alternative hypothesis.
- If p-value > α: You fail to reject the null hypothesis. The data does not provide sufficient evidence to support the alternative hypothesis.
Remember, the p-value doesn't tell you the size of the effect or if your hypothesis is true; it only informs the probability of your data assuming the null hypothesis.
What does a p-value indicate?
+
The p-value measures the evidence against a null hypothesis. A smaller p-value means less likelihood of your results occurring by chance under the null hypothesis.
How do I know which t-test to use?

+
Choose based on your data type and assumptions about variance: paired, two-sample equal variance, or two-sample unequal variance.
Can I use Excel for all types of statistical tests?

+
Excel is versatile for many basic statistical tests, but complex analyses might require specialized statistical software.
By following this guide, you’ve equipped yourself with the knowledge to compute the p-value directly in Excel, aiding you in making statistically informed decisions from your datasets. This ability to calculate and interpret p-values will undoubtedly enhance your analysis proficiency, leading to more robust conclusions. Moreover, understanding the significance of p-values fosters a deeper appreciation for the importance of hypothesis testing in research and data-driven decision-making. Keep practicing with different datasets to refine your skills in statistical analysis.