5 Easy Steps to Create a Standard Curve in Excel
Performing a standard curve analysis is an essential skill in various scientific fields, including biochemistry, pharmacology, and environmental science, where quantifying unknown concentrations of substances is a common task. Standard curves allow you to convert raw data into meaningful information, providing insights into experimental outcomes. In this guide, we'll take you through the five easy steps to create a standard curve in Excel, helping you analyze and interpret data effectively.
Step 1: Preparing Your Data
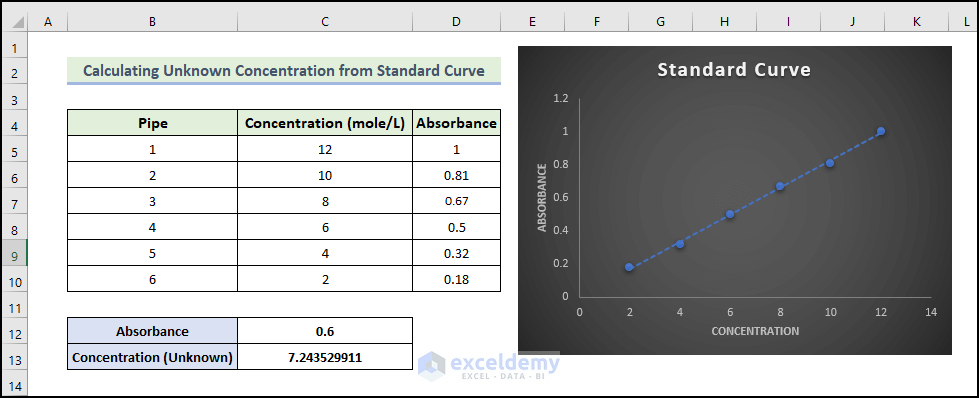
Before you dive into Excel, ensure you have your data ready. A standard curve involves a set of known concentrations (x-axis) and their corresponding measurements or signals (y-axis):
- List out the known concentrations or standards.
- Record the responses or signal for each concentration, typically in the form of absorbance, fluorescence, etc.
🔬 Note: Ensure your measurements are consistent in their units. If using absorbance, all values should be absorbance units (AU).
Step 2: Entering Data into Excel
Open a new Excel worksheet and begin inputting your data:
- In column A, enter your standard concentrations.
- In column B, enter the corresponding signal values.
Here’s a simple representation of how your table should look:
| Concentration (x) | Signal (y) |
|---|---|
| 10 | 0.5 |
| 20 | 1.0 |
| 30 | 1.5 |
Step 3: Plotting the Data
Now, let’s create the scatter plot:
- Select your data table.
- Navigate to the ‘Insert’ tab and choose ‘Scatter’ from the chart options.
- Opt for the Scatter with Straight Lines chart type.
The plot should visually represent the relationship between concentration and signal.
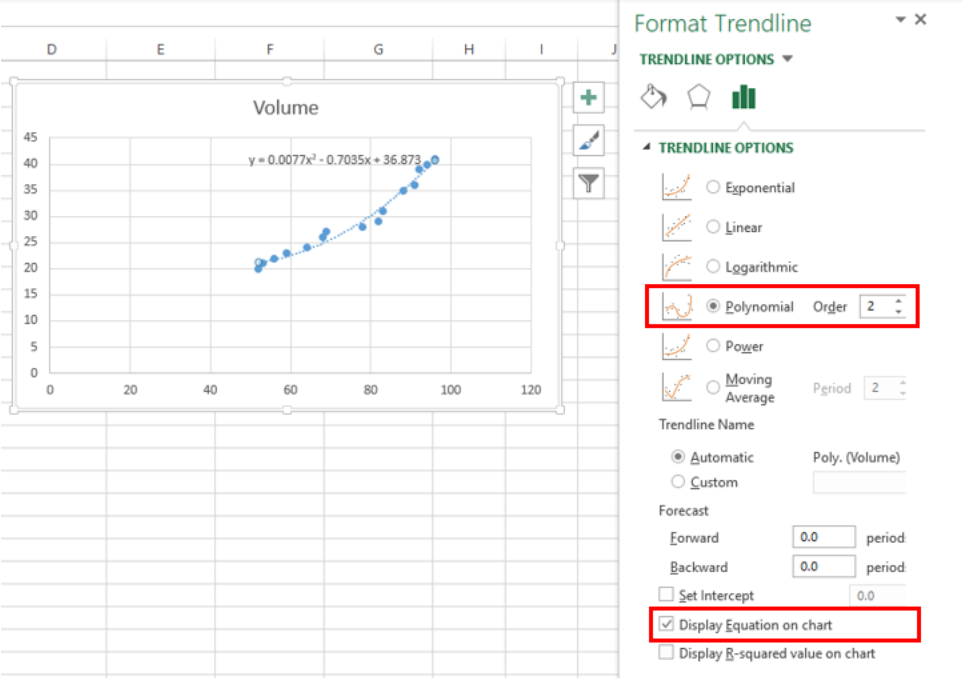
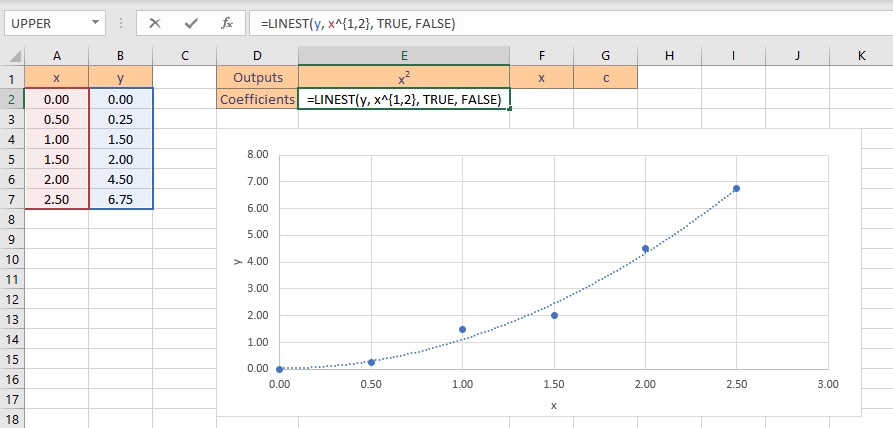
Step 4: Adding the Trendline
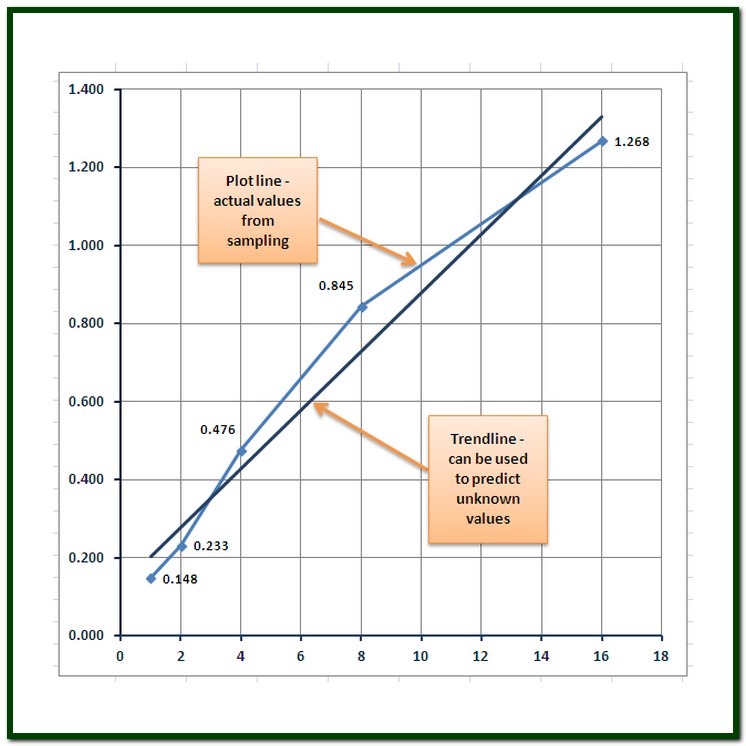
Next, add a trendline to interpret this relationship mathematically:
- Click on any data point in your scatter plot.
- Right-click, then choose ‘Add Trendline’ from the dropdown menu.
- Select ‘Linear’ as the trendline type.
- Under ‘Options’, check the boxes for ‘Display Equation on chart’ and ‘Display R-squared value on chart’.
This step quantifies the linear relationship between the concentration and signal, offering you the equation of the line and the coefficient of determination (R²).
📈 Note: The closer the R² value is to 1, the better the fit of the line to the data, indicating higher accuracy in concentration estimations.
Step 5: Interpreting the Results
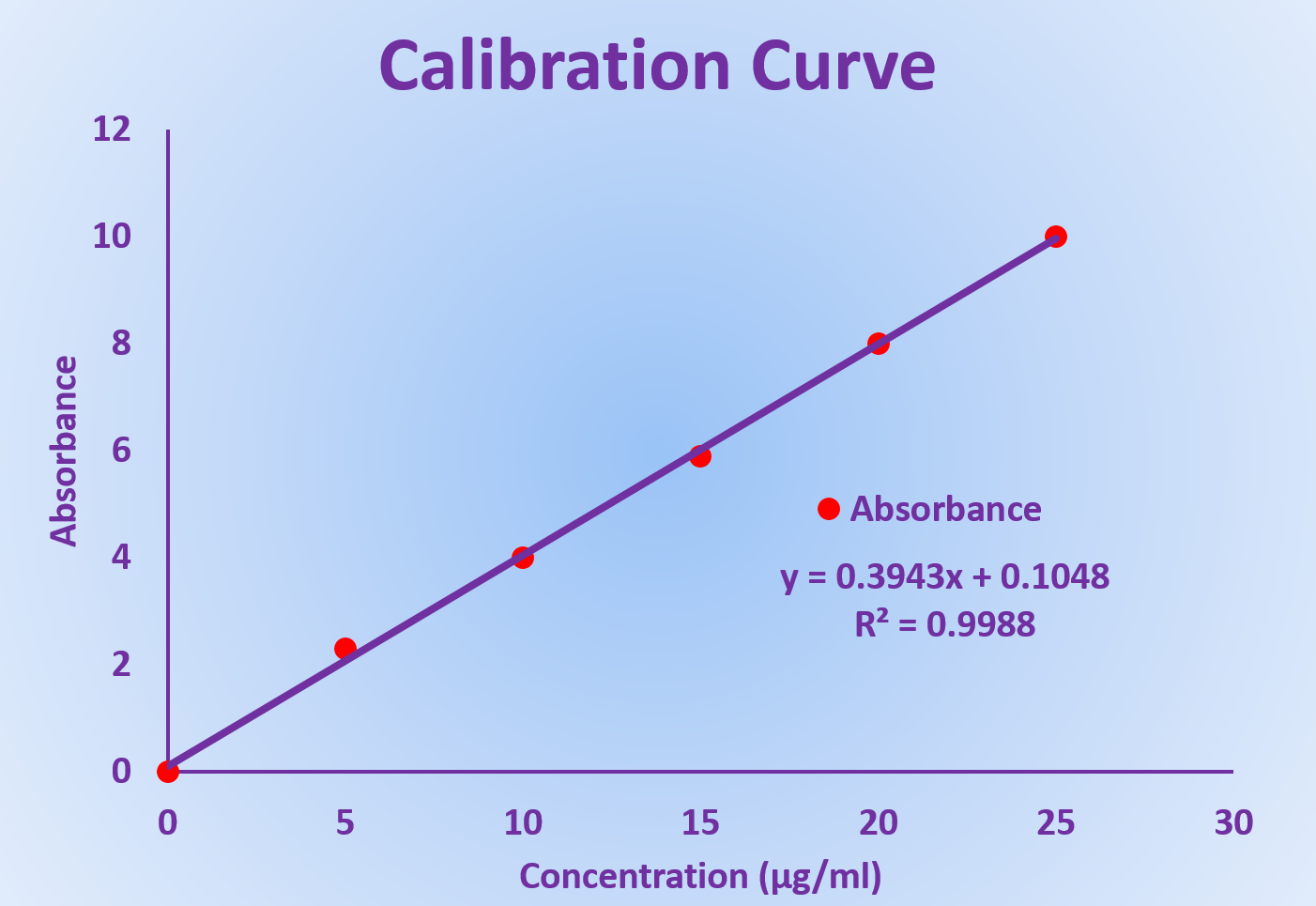
With the trendline in place, interpreting the results becomes more scientific:
- The equation of the line gives you the linear relationship between concentration and signal.
- Using this equation, you can estimate the concentration of unknown samples by inputting their signal values into the equation.
The R² value indicates how well the standards predict the unknown values, with higher values suggesting better predictive power.
In summary, creating a standard curve in Excel involves collecting and preparing data, entering it into Excel, plotting the data, adding a trendline, and interpreting the results. This process allows you to understand the relationship between concentration and signal, providing a reliable method for quantifying unknown samples in your experiments.
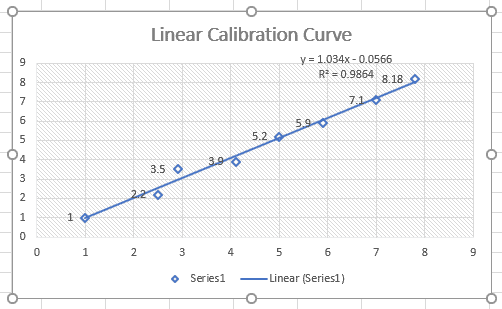
Why do I need a standard curve?
+
A standard curve is essential for quantifying unknown samples. It allows you to convert signal values (like absorbance or fluorescence) to concentration, which is crucial in scientific experiments to understand the amount of analyte present.
What does the R-squared (R²) value indicate?
+
The R-squared value, also known as the coefficient of determination, indicates how well the standards fit the linear model. A value closer to 1 suggests a strong predictive relationship between the standards and the unknown samples.
Can I use a non-linear trendline for my standard curve?

+
Yes, if the relationship between concentration and signal isn’t linear, you can choose other trendline options like polynomial, logarithmic, or exponential to better fit your data. However, linear relationships are often preferred due to their simplicity and straightforward interpretation.
How can I ensure the accuracy of my standard curve?
+
To ensure accuracy, use high-quality standards, replicate each concentration to account for variability, and check for any signs of saturation or deviation from linearity. Also, consider running known controls alongside your samples to validate the curve.
What if my signal is outside the range of my standard curve?
+
If your signal falls outside the range, you should re-evaluate your experimental design. Either dilute the sample to bring it within the curve’s range or prepare additional standards at higher concentrations to extend the linear range of the curve.