5 Simple Steps to Calculate P-Value in Excel
In the realm of statistical analysis, the p-value plays an indispensable role, especially when determining the significance of results from hypothesis tests. Excel, with its suite of data analysis tools, provides a straightforward way to calculate the p-value for various statistical tests. Here, we will guide you through five simple steps to calculate the p-value in Excel, making the process accessible even for those who may not have a deep background in statistics.
Step 1: Data Collection and Entry

The first step in calculating a p-value in Excel involves data collection. Whether you’re analyzing the effect of a new fertilizer on plant growth or assessing the impact of a marketing campaign, ensure that:
- Data is accurate and representative.
- Input your data into Excel carefully, avoiding errors or omissions.
📝 Note: Accuracy in data entry prevents flawed results. Check your data twice!
Step 2: Identify the Hypothesis and Test

Understanding the hypothesis and selecting the correct statistical test is crucial:
- Hypothesis: Identify your null (H0) and alternative (H1) hypotheses.
- Test: Decide on the type of statistical test you need to perform (e.g., t-test for means, chi-square for categorical data).

📝 Note: Selecting the wrong test can lead to incorrect conclusions. Cross-check your choice with statistical resources or experts.
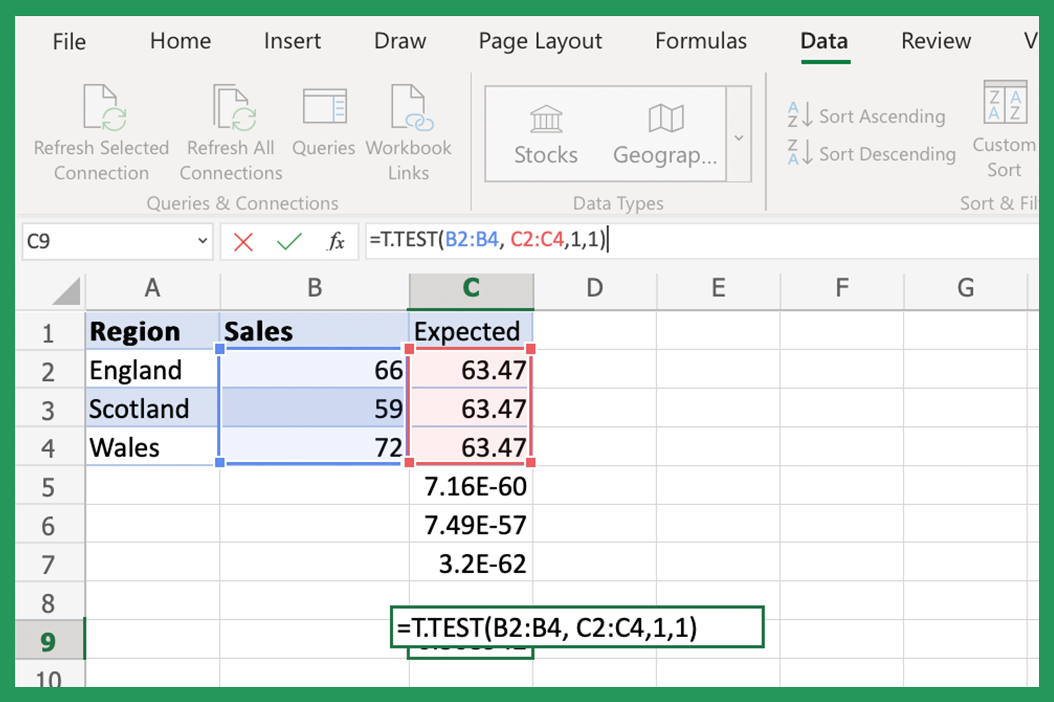
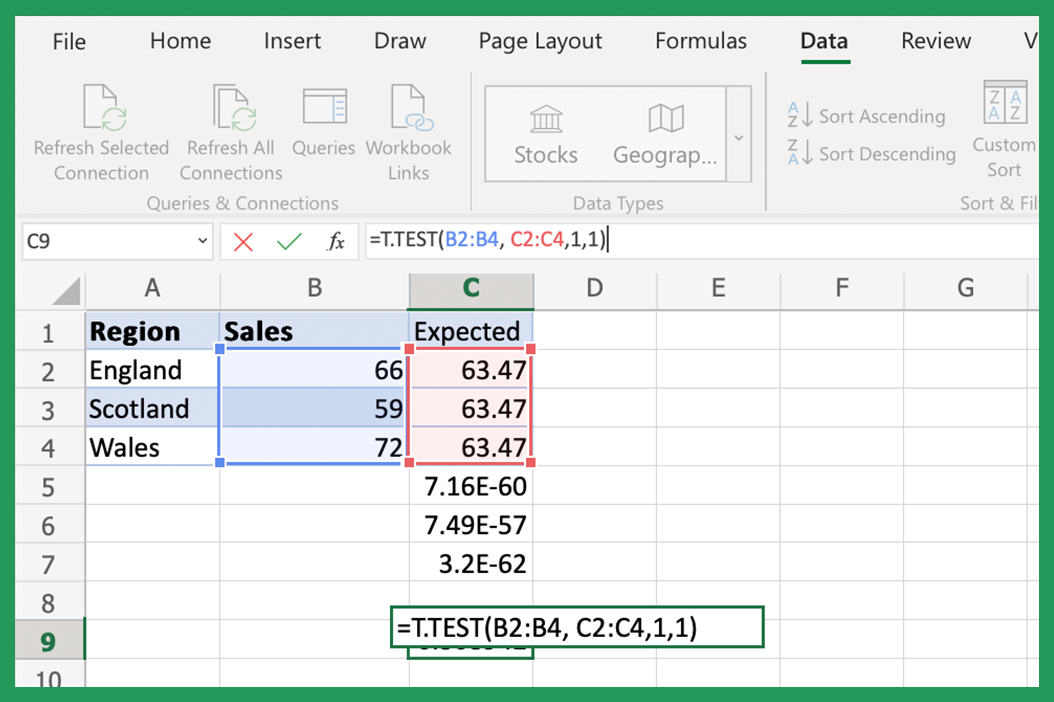
Step 3: Conduct the Statistical Test
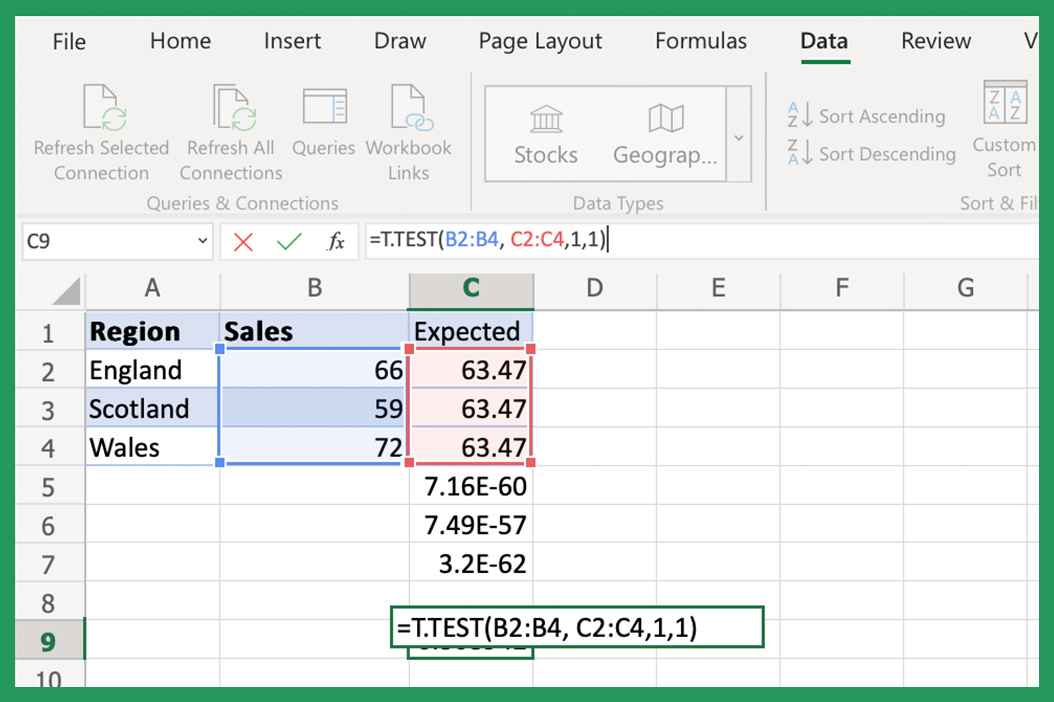
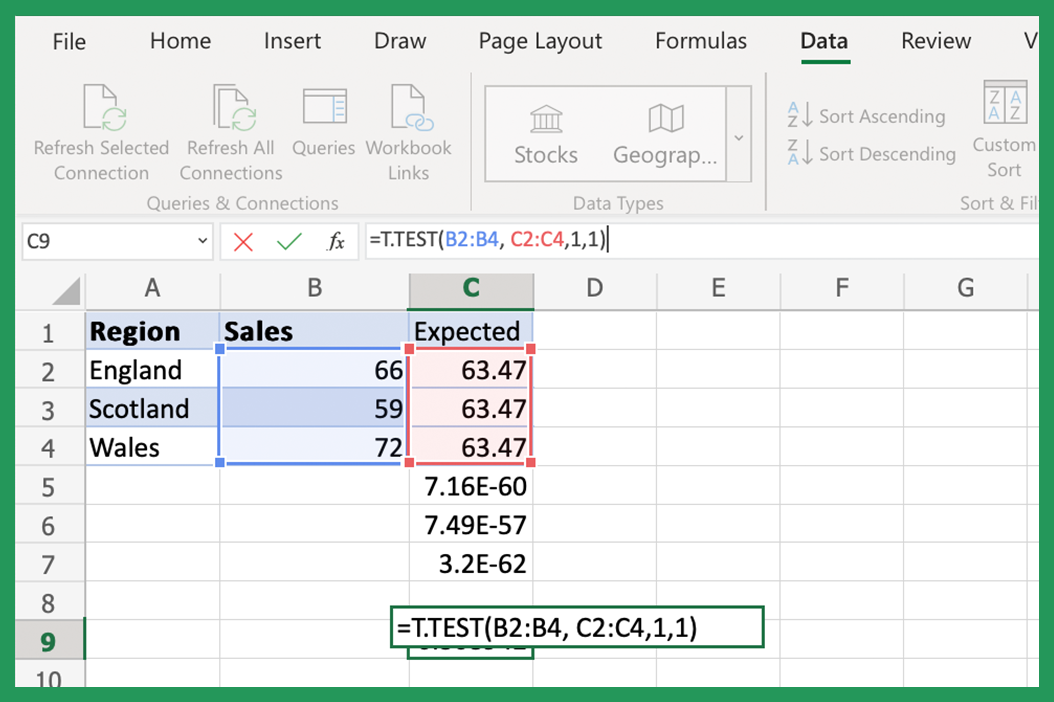
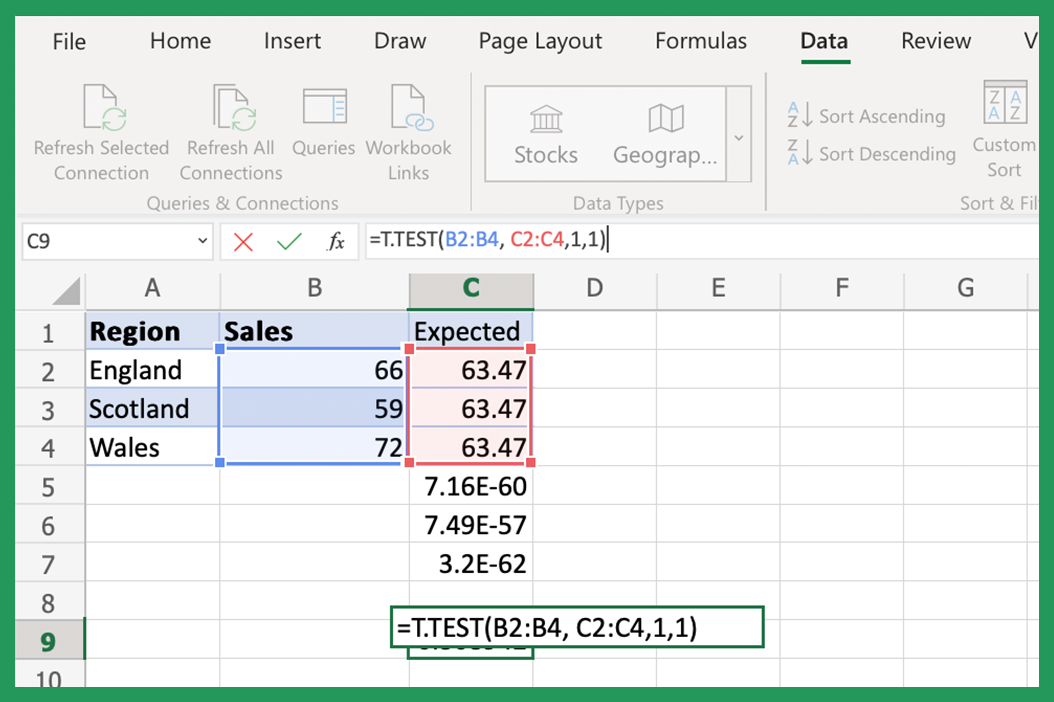
Once you have your data and hypothesis:
- Go to the “Data” tab and click on “Data Analysis.”
- Select the appropriate test (e.g., “t-Test: Two-Sample Assuming Equal Variances”).
- Fill in the required fields with your data ranges, specifying if your test is one-tailed or two-tailed.
- Excel will compute various statistics, including the test statistic.
Here’s a table summarizing the steps:
| Step | Description |
|---|---|
| 1 | Navigate to Data Analysis |
| 2 | Select Test |
| 3 | Enter Data Ranges |
| 4 | Compute Statistics |
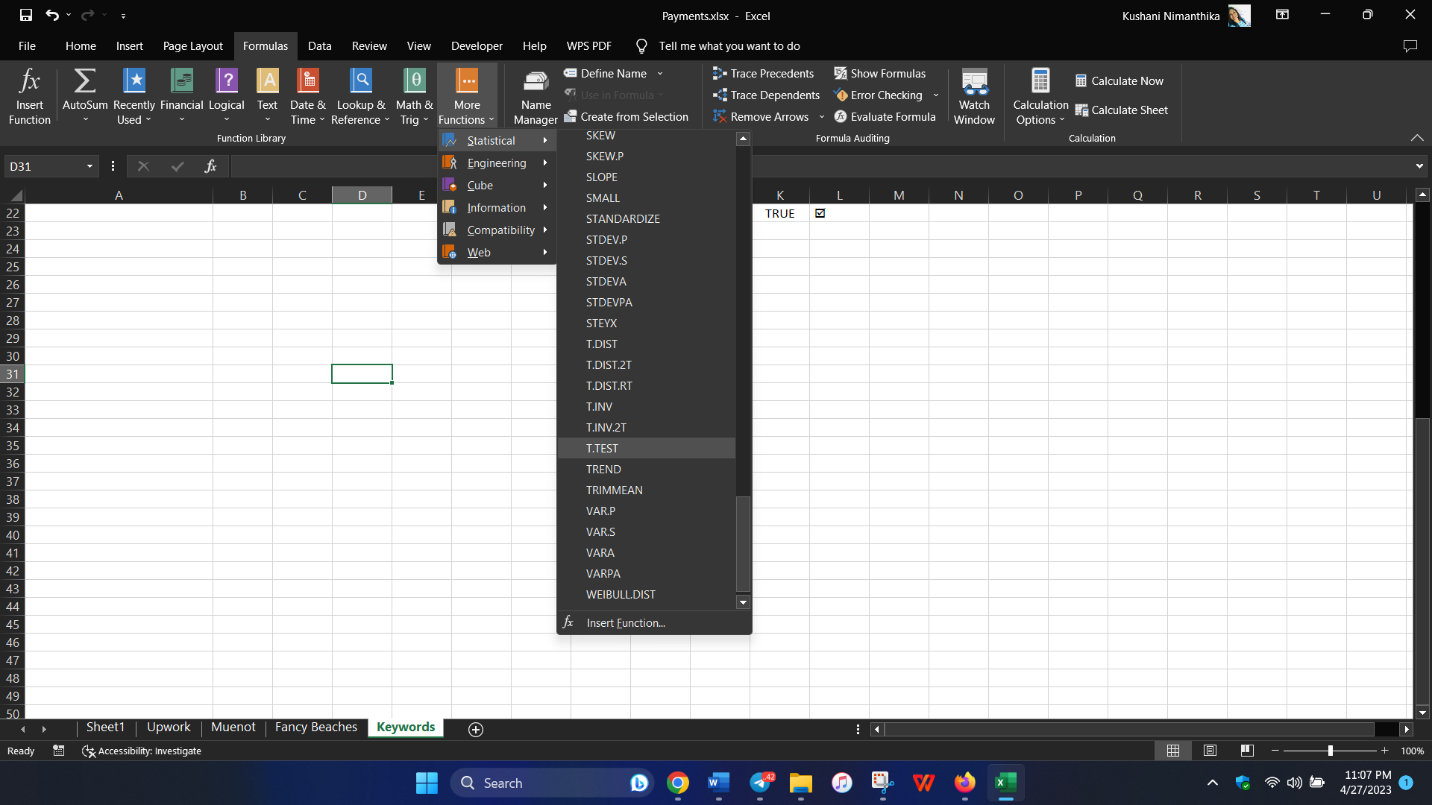
📝 Note: Ensure you understand the difference between one-tailed and two-tailed tests.
Step 4: Interpret the P-Value

After conducting the test, Excel will display the p-value:
- Null Hypothesis (H0): A p-value below a predetermined significance level (often 0.05) indicates you can reject H0.
- Statistical Significance: A p-value of 0.05 means there is a 5% chance of obtaining the observed results if H0 were true.
📝 Note: Misinterpreting p-values is a common statistical mistake. A low p-value doesn’t prove your hypothesis; it suggests that H0 is unlikely.
Step 5: Communicate Your Findings
Finally, present your findings:
- Summarize your results using tables or charts to visualize the data and p-value.
- Discuss the implications of your findings, ensuring to contextualize the p-value within the broader context of your research.
📝 Note: Effective communication is key in statistics. Make your presentation clear and accessible to your intended audience.
In summary, calculating a p-value in Excel involves meticulous data entry, understanding your hypothesis, choosing the right test, interpreting results correctly, and effectively communicating your findings. By following these steps, even those not deeply entrenched in statistical analysis can harness the power of Excel to draw meaningful conclusions from their data. This process not only informs decision-making but also enhances the understanding of the underlying statistical principles that govern how we interpret data in the modern world.
What does a p-value actually tell us?
+
A p-value indicates the probability of observing the results (or more extreme results) assuming that the null hypothesis is true. It does not measure the size of an effect or the probability that the alternative hypothesis is true.
Can I use Excel for all statistical tests?

+
Excel offers basic statistical functions and tools but is not as comprehensive as specialized statistical software like SPSS or R. For more complex tests or large datasets, consider using dedicated statistical software.
How should I set the significance level?
+
The significance level, often denoted as alpha (α), is typically set at 0.05 by convention. However, it can be adjusted based on the context of the study, the risk associated with incorrect decisions, or the nature of the hypotheses being tested.