5 Steps to Master Chi-Square Tests in Excel
Mastering Chi-Square Tests in Microsoft Excel is a valuable skill for anyone delving into data analysis, particularly when dealing with categorical data. Whether you are a researcher, data analyst, or a student, understanding how to execute and interpret these tests can greatly enhance your data literacy. Here's an in-depth guide on performing Chi-Square Tests in Excel to help you conduct sound statistical analyses.
Understanding the Chi-Square Test
Before we dive into the mechanics, it’s crucial to grasp what Chi-Square Tests are:
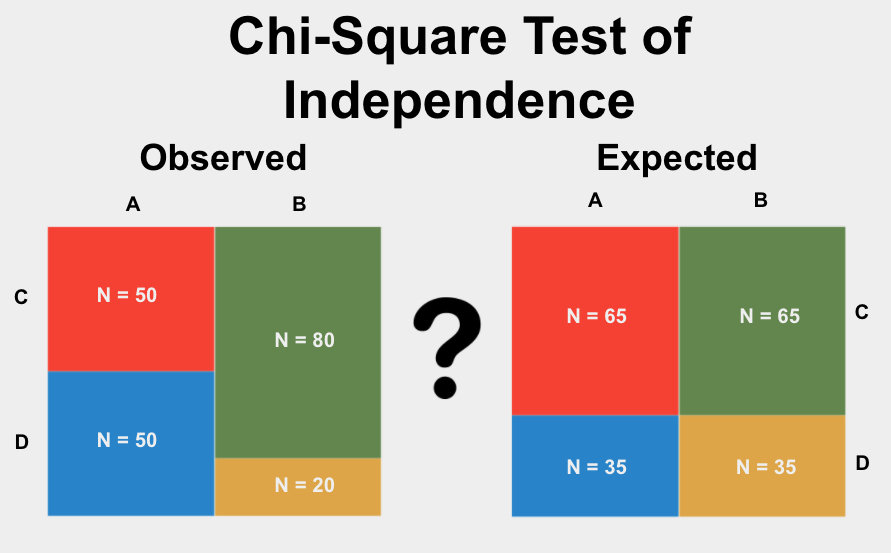
- Purpose: Chi-Square Tests are used to determine if there is a significant association between categorical variables.
- Types: There are two main types - Chi-Square Test of Independence and Goodness of Fit.
- Assumptions: The data should be randomly sampled, each variable should be categorical, and expected frequency should be at least 5 for each cell.

Now, let’s walk through the process of executing a Chi-Square Test in Excel.
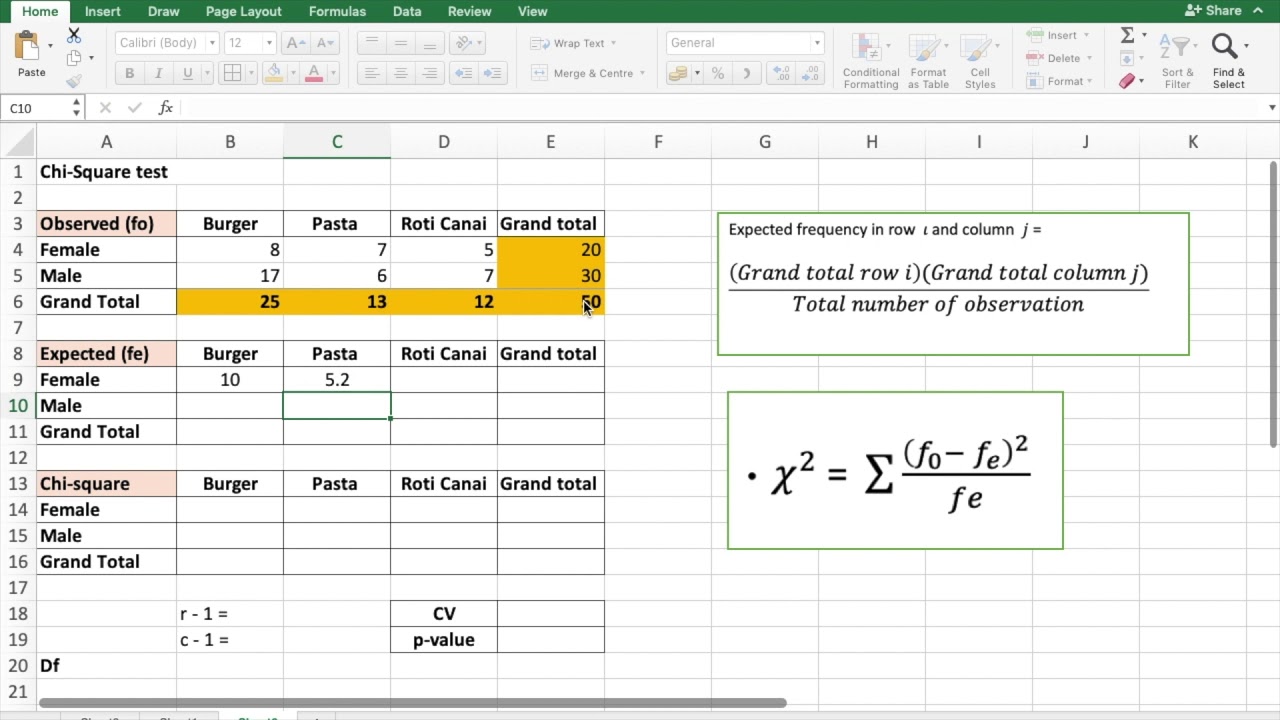
Step 1: Data Preparation
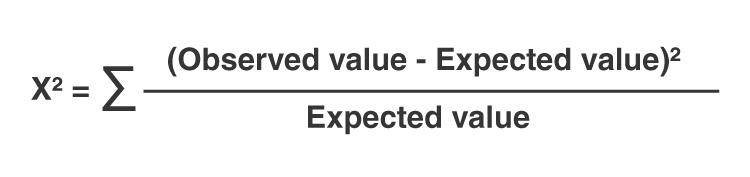
Proper data preparation is key to accurate Chi-Square testing:
- Organize your data into a tabular format with rows and columns representing the categories.
- Ensure there are no missing values in the dataset.
- If necessary, create a contingency table or cross-tabulation.
Step 2: Input Data into Excel
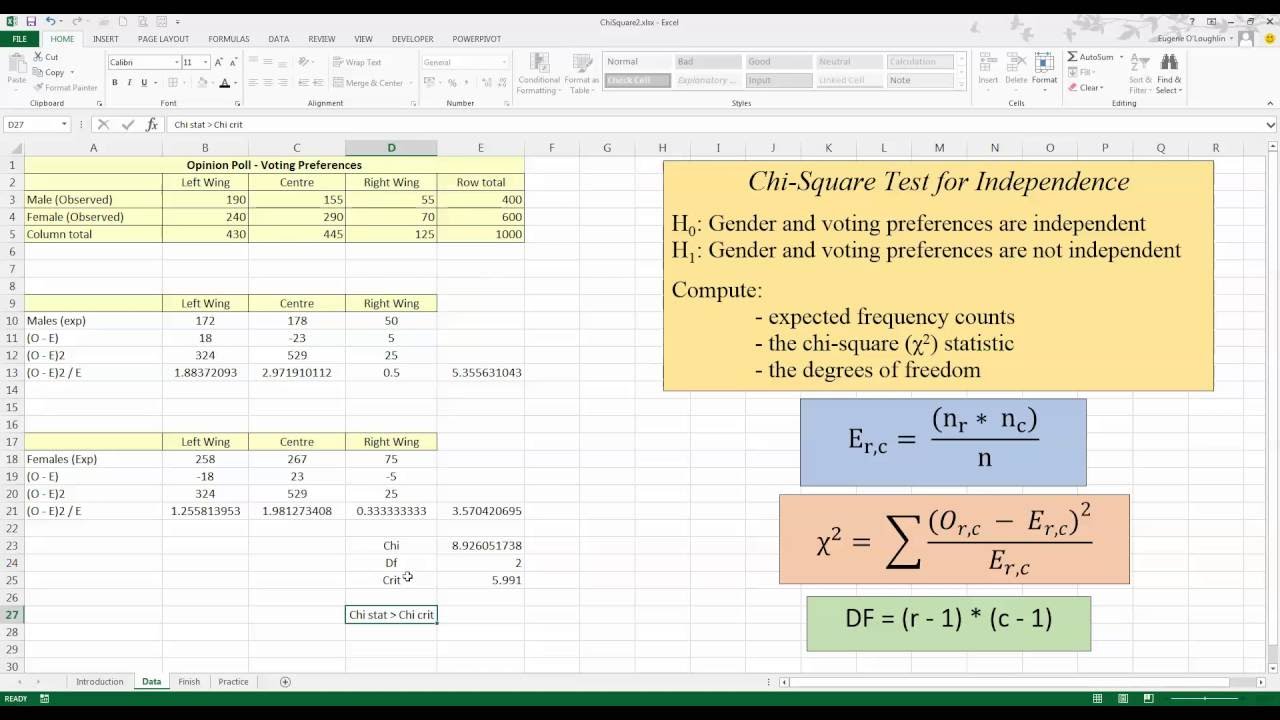
Begin by setting up your data:
- Enter your observed frequencies into an Excel worksheet.
- Make sure to label the rows and columns correctly for clarity.
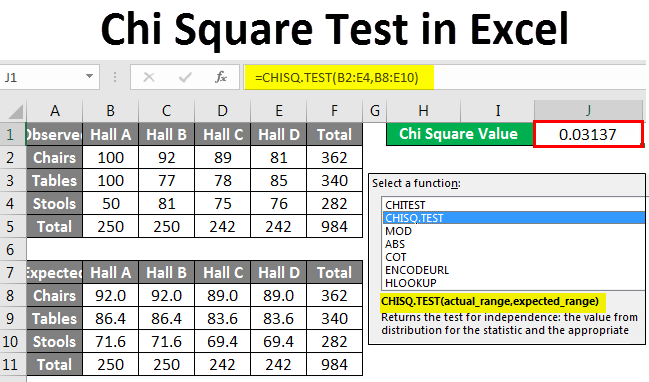
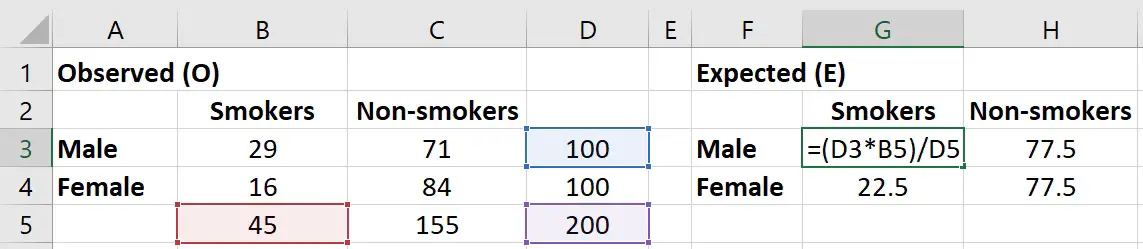
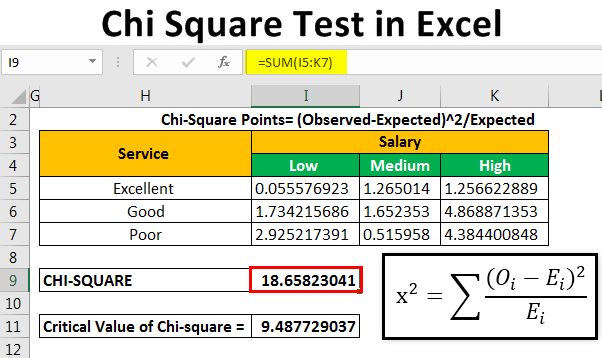
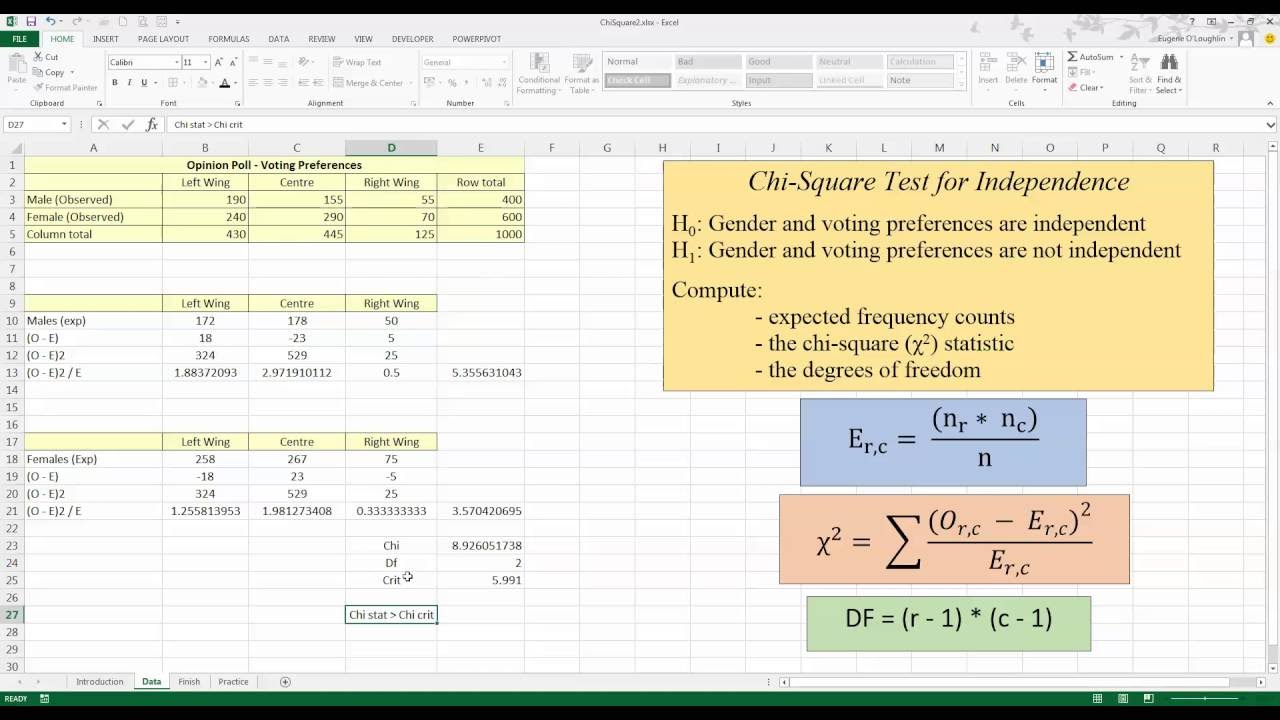
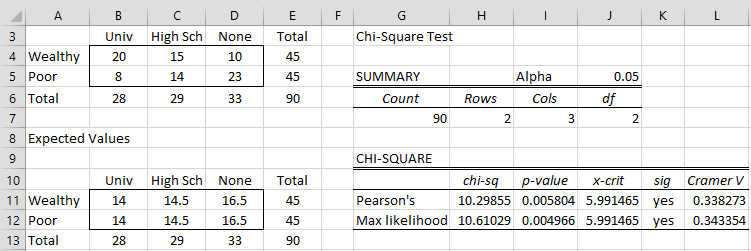
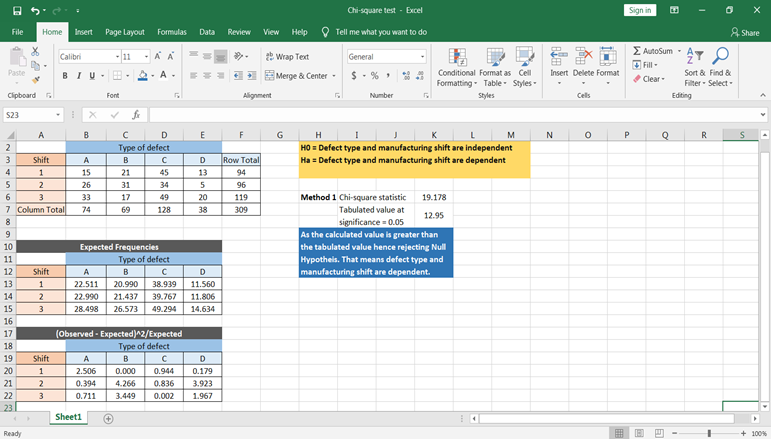
Step 3: Calculate Expected Frequencies
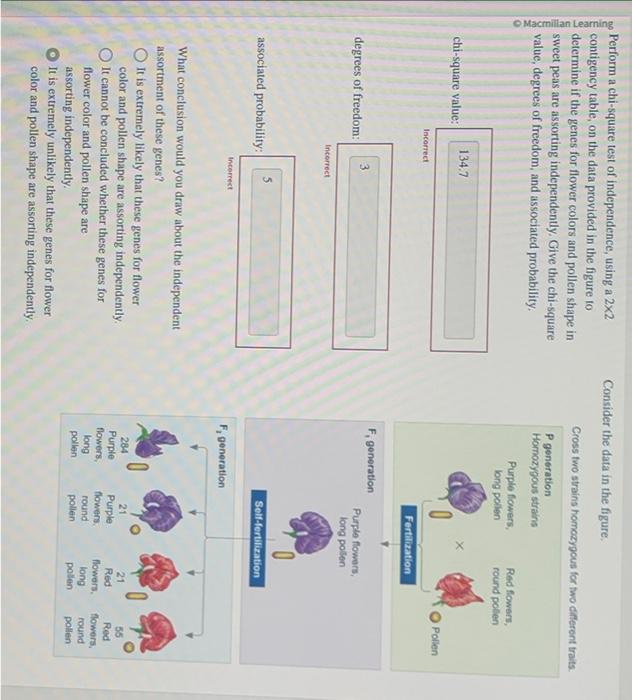
Expected frequencies are calculated as follows:
| Formula | Description |
|---|---|
| (Row Total * Column Total) / Grand Total | Calculate each cell’s expected frequency based on marginal totals. |
📝 Note: Always verify your expected frequencies against the sum of all cells to ensure accuracy.
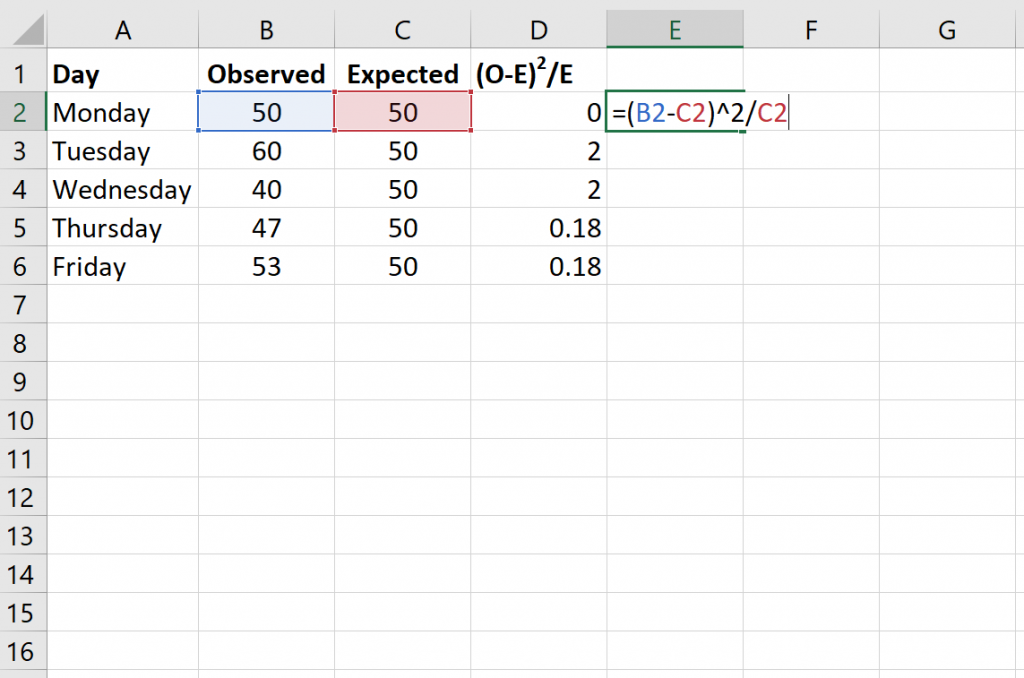
Step 4: Calculate the Chi-Square Statistic
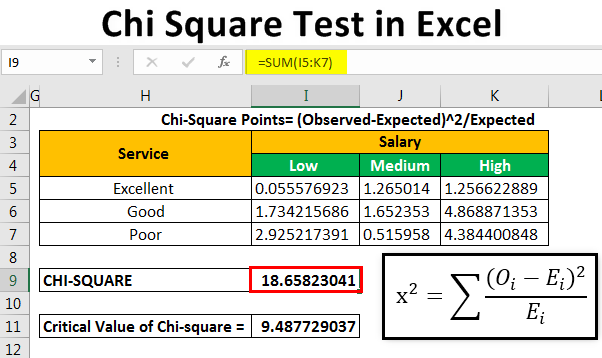
Use Excel’s functions to compute the Chi-Square statistic:
- Use the formula: Chi-Square = Σ[(Observed - Expected)^2 / Expected]
- Input this into an Excel cell or create a formula that calculates this sum over the dataset.
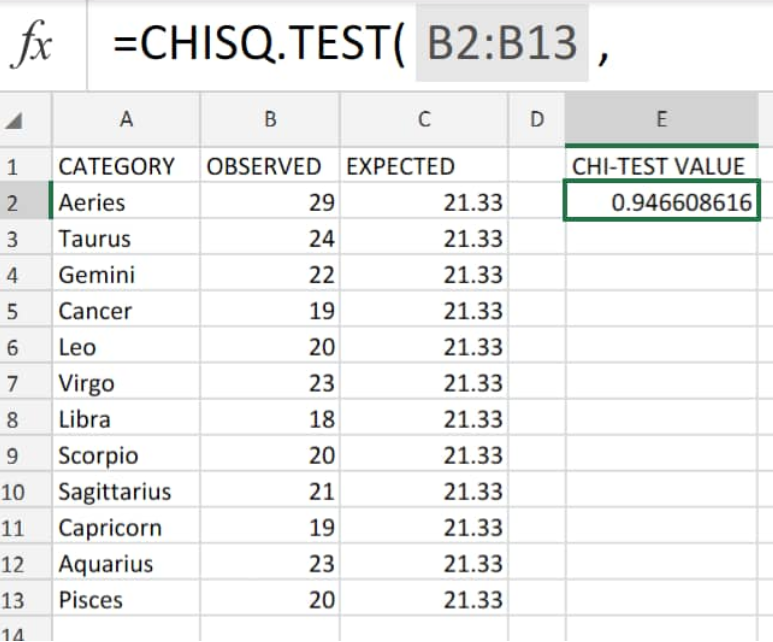
Step 5: Determine the P-value
Once you have the Chi-Square statistic:
- Use Excel’s
CHIDISTorCHISQ.DIST.RTfunction to find the p-value. - Compare the p-value to your chosen significance level (commonly 0.05) to determine significance.
Interpreting the results is critical:
- If p-value ≤ significance level: Reject the null hypothesis.
- If p-value > significance level: Fail to reject the null hypothesis.
Final Thoughts
Mastering Chi-Square Tests in Excel allows you to explore categorical data with confidence. From understanding the underlying principles to preparing your data and interpreting results, you've now taken significant steps towards becoming proficient in statistical analysis. This proficiency not only aids in academic and research environments but also enhances your ability to make data-driven decisions in professional settings.
What does the Chi-Square Test tell me?
+
The Chi-Square Test tells you whether there’s a statistically significant difference between the expected frequencies and the observed frequencies in one or more categories. This test helps you understand if the associations between categories are by chance or if there is a significant relationship.
How do I know which significance level to use?
+
The choice of significance level depends on how stringent you want to be with your statistical test. Commonly used levels are 0.05, 0.01, and sometimes 0.10. The level of 0.05 is widely accepted for most fields.
Can I perform a Chi-Square Test on continuous data?
+
No, Chi-Square Tests are designed for categorical (nominal) data only. If you have continuous data, you would first need to categorize or bin the data before applying a Chi-Square Test.
What if my expected frequencies are less than 5?
+
If any cell in your contingency table has an expected frequency less than 5, the Chi-Square Test might not be reliable. You might need to combine categories to increase expected frequencies or consider using a different test like Fisher’s Exact Test for 2x2 tables.
How can I ensure my data meets the assumptions for Chi-Square Tests?
+
Ensure your data is randomly sampled, each category is mutually exclusive, and the total sample size is adequate to have at least 5 expected observations per cell. If these assumptions aren’t met, consider adjusting your dataset or methodology.