5 Easy Ways to Find P Value in Excel
Whether you're a student, a researcher, or a data analyst, understanding how to calculate the p-value is crucial for interpreting the significance of your data. Excel, known for its versatility in data analysis, offers several tools and functions to perform statistical tests and find p-values. This guide will explore five straightforward methods to calculate p-values in Microsoft Excel, ensuring that you can apply statistical analysis with ease.
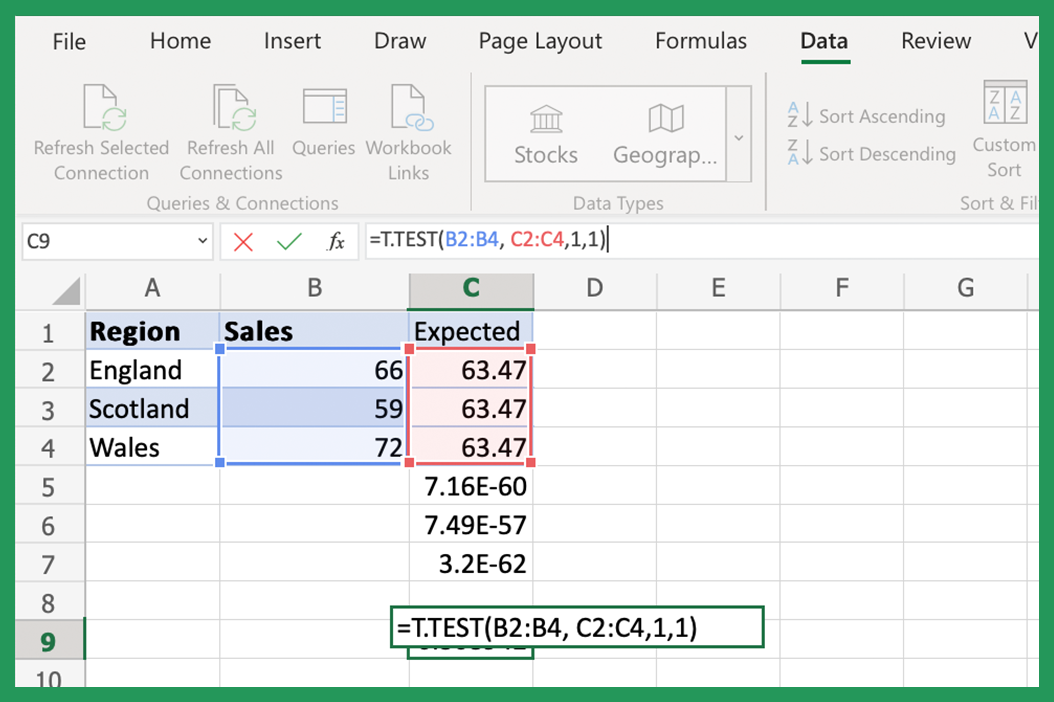
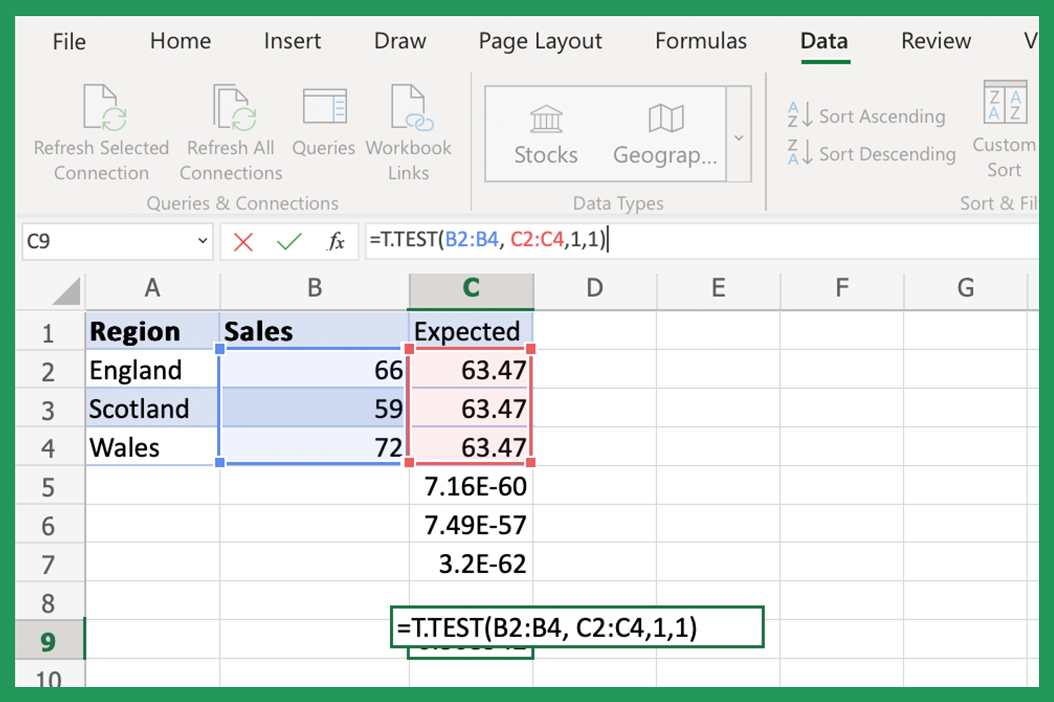
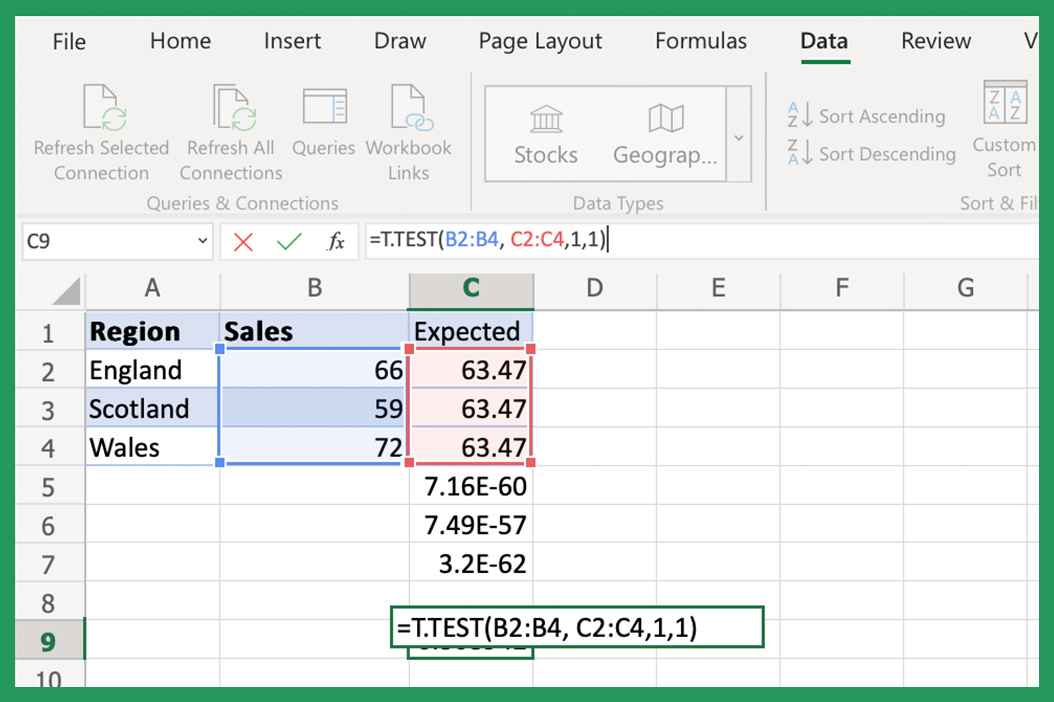
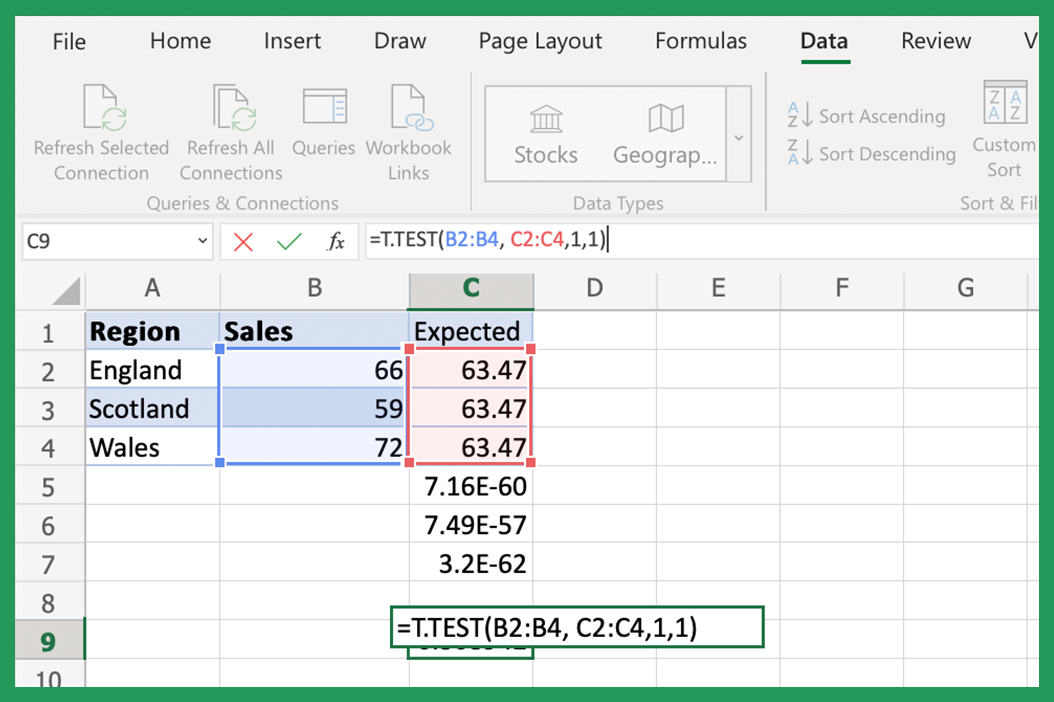
1. Using the T-TEST Function for Independent Samples

The T.TEST function in Excel computes the p-value for testing the hypothesis that two independent samples come from populations with the same mean. Here's how to use it:
- Select Data: Ensure your two sample datasets are in columns next to each other or in separate ranges.
- Formula Syntax: The function's syntax is
=T.TEST(array1, array2, tails, type). - Enter Data: Replace 'array1' and 'array2' with the actual cell ranges for your datasets, 'tails' determines whether it's a one-tailed or two-tailed test, and 'type' specifies if it's a paired, homoscedastic, or heteroscedastic test.
- Interpret Results: The returned value is the p-value, which you can compare against your significance level to accept or reject the null hypothesis.
Example:
If you have two sets of data in ranges A1:A10 and B1:B10, you might use:
=T.TEST(A1:A10, B1:B10, 2, 2) for a two-tailed test assuming unequal variances.
💡 Note: Remember to check the significance level (commonly 0.05) to determine if the p-value indicates significance.
2. Chi-Square Test for Independence
The CHISQ.TEST function in Excel helps assess if there's a significant association between categorical variables:
- Data Setup: Arrange your observed and expected frequencies in a contingency table.
- Formula: Use
=CHISQ.TEST(observed_range, expected_range). - Analysis: Excel returns the p-value, which you'll compare to your chosen significance level.
📌 Note: Ensure that the expected frequencies are theoretical or calculated based on assumptions.
3. Z-Test for One Sample Mean
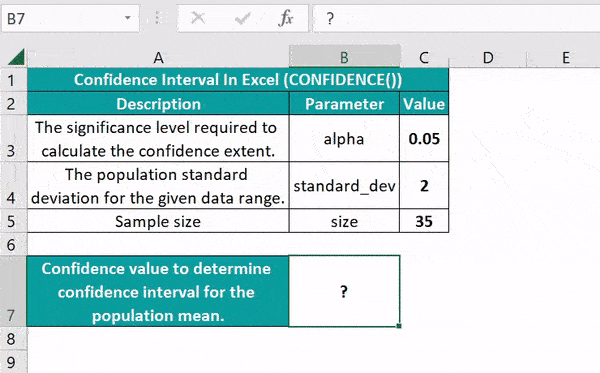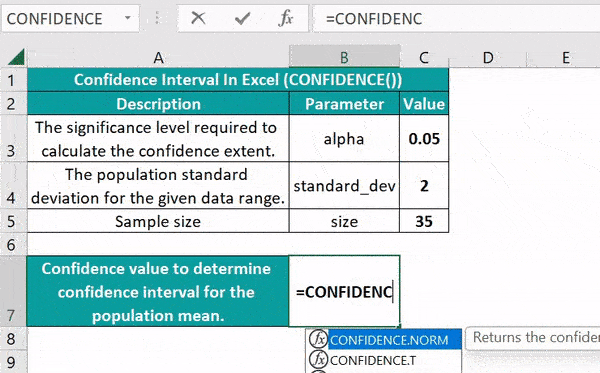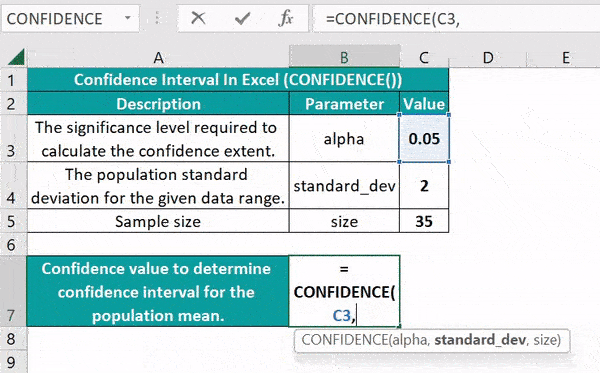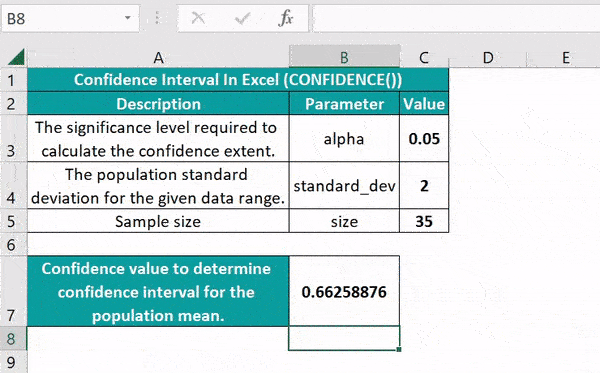
If you're dealing with large sample sizes and normality can be assumed, Excel provides tools for a Z-Test:
- Data Input: Use the Z.TEST function with the following structure:
- Formula:
=Z.TEST(array, x, [sigma])where 'array' is your sample data, 'x' is the hypothesized mean, and 'sigma' is the population standard deviation (optional). - Result: The p-value will be returned, indicating the probability of observing your results if the null hypothesis were true.
Example:
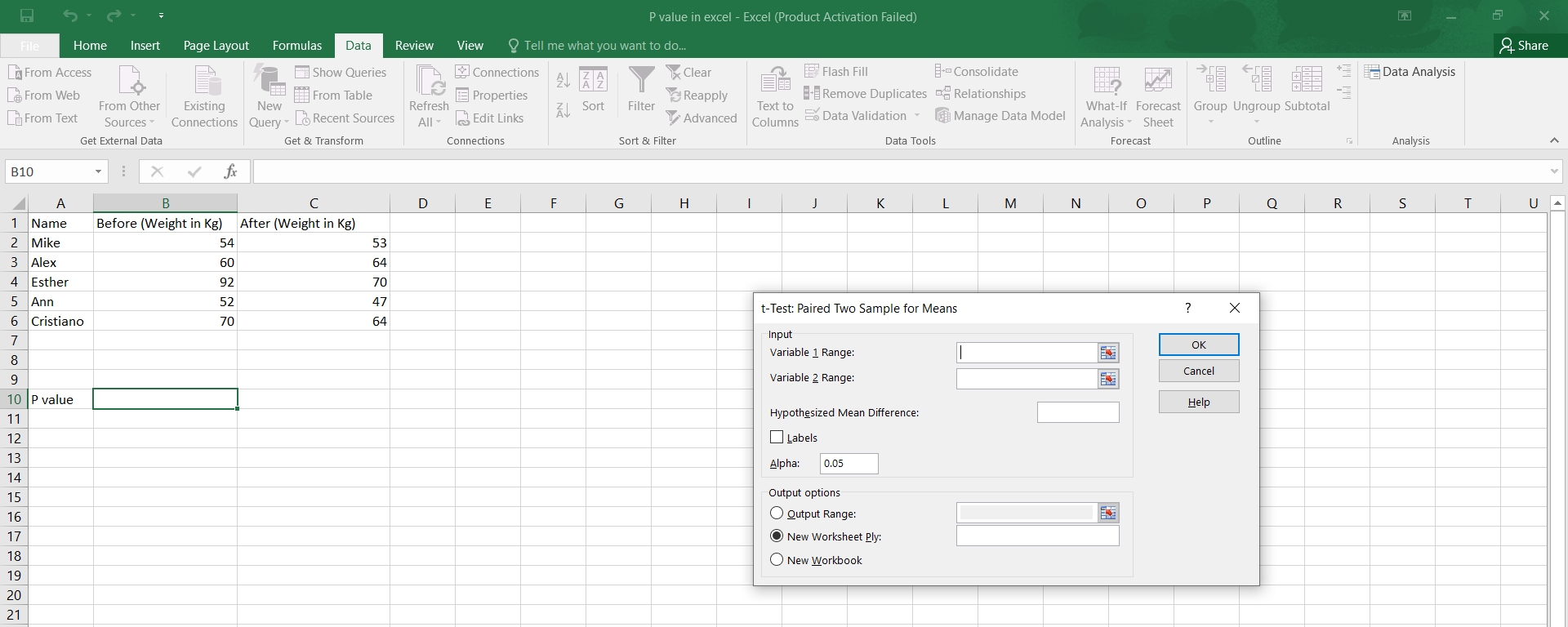
To test if the mean IQ score of a group is 100 with your data in A1:A20, you’d use:
=Z.TEST(A1:A20, 100)
💡 Note: If sigma is unknown, it's often estimated from the sample itself, leading to a different formula known as the t-test.
4. Using ANOVA for Comparing Multiple Groups
Analysis of Variance (ANOVA) is useful for comparing means of more than two groups:
- Data Arrangement: Stack your data in one column and use another for group identifiers.
- Analysis ToolPak: Enable this add-in if not already active under Excel Options > Add-Ins.
- Anova Tool: Under Data Analysis, select ANOVA: Single Factor or Two-Factor.
- Interpreting Results: Look for the 'P-value' in the ANOVA table to determine significance.
Here's a sample layout:
| Group | Data |
|---|---|
| 1 | 10 |
| 1 | 12 |
| 2 | 15 |
| 2 | 18 |

💡 Note: If you're comparing two groups with ANOVA, remember that the results are equivalent to a two-sample t-test.
5. Using Regression Analysis for Correlation

To find the p-value associated with the correlation coefficient, you can perform regression analysis:
- Data: Enter your X and Y variables in separate columns.
- Toolpak Activation: Ensure the Analysis ToolPak is active.
- Regression Tool: Go to Data Analysis > Regression.
- P-Value: The regression output will include the p-value for each coefficient, allowing you to assess the significance of predictors.
📌 Note: The p-value in regression analysis corresponds to the t-statistic for each variable, showing if the relationship between the variable and the response is statistically significant.
By mastering these five methods, you'll have a robust toolkit for conducting statistical tests and interpreting results in Excel. From comparing two sample means with T-TEST to exploring correlations through regression, Excel provides a straightforward way to delve into statistical analysis without needing advanced software. The ease of these methods allows for quick analysis and decision-making, enhancing your data interpretation skills significantly.
What is the difference between a one-tailed and two-tailed test in Excel?

+
In a one-tailed test, you are looking for an effect in one direction only (e.g., whether one group performs better than another). In a two-tailed test, you are checking if there’s a difference in either direction, which is commonly used when you’re not predicting the direction of the effect.
Can Excel perform non-parametric tests?

+
Excel’s built-in functions are mainly designed for parametric tests. For non-parametric tests, you might need to use statistical software or add-ins like the Real Statistics Resource Pack or perform calculations manually.
How do I interpret the p-value?

+
A p-value less than your significance level (commonly set at 0.05) suggests that you reject the null hypothesis, indicating that your results are statistically significant. Conversely, a higher p-value means there isn’t enough evidence to reject the null hypothesis.
Is it possible to calculate p-values for multiple comparisons in Excel?
+
Yes, using ANOVA for multiple comparisons or through pairwise comparisons with t-tests or other methods. However, for complex multiple comparison corrections like Bonferroni or Holm-Bonferroni, you might need to do some manual adjustments or use external tools.