5 Ways to Calculate P Value in Excel Easily
5 Ways to Calculate P-Value in Excel Easily

If you're delving into the world of statistical analysis, understanding how to calculate the P-value in Excel can be crucial. The P-value helps determine the statistical significance of your data and whether to accept or reject a null hypothesis. Here are five straightforward methods to compute the P-value in Excel, ensuring you can perform these calculations with ease and accuracy.
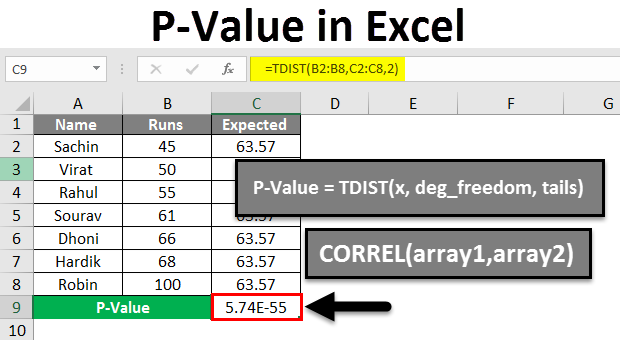
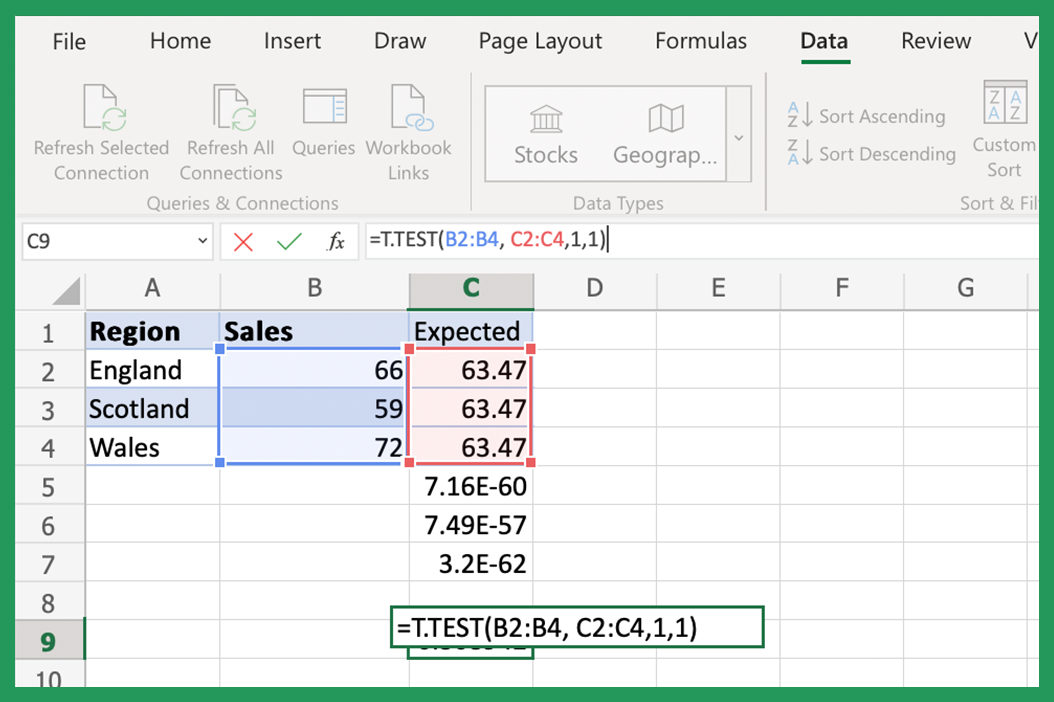
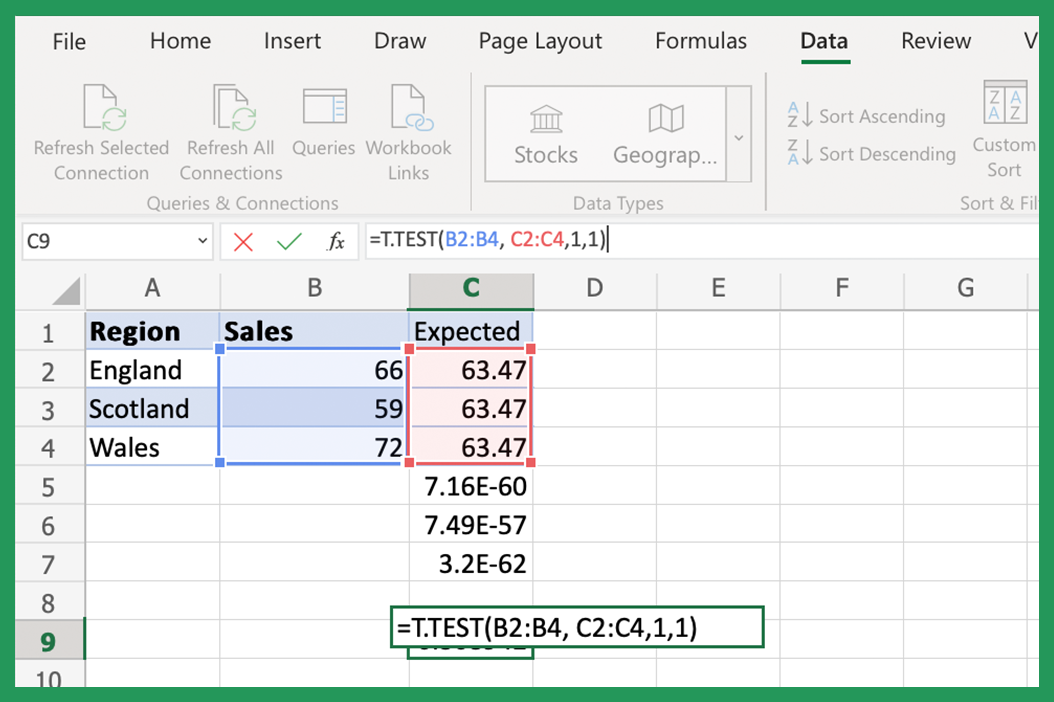
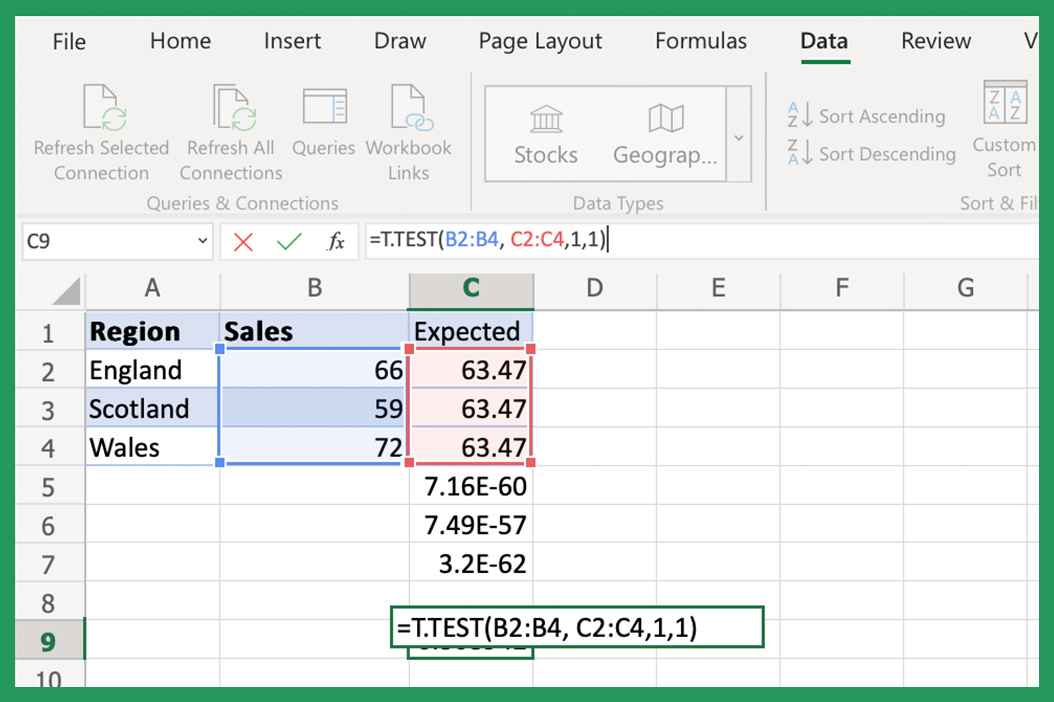
1. Using T.TEST Function for Two-Sample Testing

The T.TEST function in Excel is designed for comparing the means of two groups, often used when you want to test the hypothesis that the means of two independent samples are equal. Here’s how to use it:
- Array1: This is the first sample data range.
- Array2: This is the second sample data range.
- Tails: Decide if your test is one-tailed (1) or two-tailed (2).
- Type: Choose the type of t-test you want to perform (1 = Paired, 2 = Two-sample equal variance, 3 = Two-sample unequal variance).
Example Syntax:
=T.TEST(array1, array2, tails, type)
📘 Note: For paired samples, use 1 for the type argument; for two independent samples with equal variances, use 2; and for unequal variances, use 3.
2. Calculating P-Value with Z.TEST Function

The Z.TEST function is used when you know the population variance and you want to test the hypothesis that the sample mean significantly differs from the population mean. Here’s how you can implement it:
- Array: The range of your dataset.
- X: The value you want to test against (usually the mean).
- Sigma: The population standard deviation (optional, if known).
Example Syntax:
=Z.TEST(array, x, [sigma])
📘 Note: If the sigma is unknown, Excel assumes the standard deviation of the array for calculation.
3. Using F.TEST for Variance Comparison
If your hypothesis involves comparing variances of two populations, the F.TEST function comes in handy:
- Array1: Range of the first dataset.
- Array2: Range of the second dataset.
Example Syntax:
=F.TEST(array1, array2)
The F.TEST function returns the right-tailed probability that comes from the F distribution. Remember, this function tests for the equality of variances.
4. CHISQ.TEST for Independence Testing
The CHISQ.TEST function is used for categorical data to test for independence or association between two or more categorical variables:
- Actual_range: The range of your observed data.
- Expected_range: The range where you provide or calculate the expected frequencies.
Example Syntax:
=CHISQ.TEST(actual_range, expected_range)
This function provides the probability associated with the Chi-square test statistic.
5. Using ANOVA and P-Value from Analysis ToolPak
For complex data analysis, Excel’s Analysis ToolPak offers ANOVA features that can be utilized:
- Enable the ToolPak in Excel’s Add-Ins.
- Go to Data > Data Analysis > ANOVA: Single Factor for one-way ANOVA, or Two-Factor with Replication for more complex analysis.
- After setting up your ANOVA, the results will include P-values.
📘 Note: The output from ANOVA will list the P-value, often under the name of ‘P-value’ or ‘Significance F’.
In summary, calculating P-values in Excel can be done effectively using built-in functions tailored to different types of data analysis. Whether you’re dealing with mean comparisons, variance tests, or categorical data, Excel offers robust tools to facilitate these calculations. Understanding the appropriate function to use based on your dataset’s characteristics can greatly enhance the accuracy and depth of your statistical analysis.
Why is P-value important in statistical testing?

+
The P-value indicates the strength of the results, helping to determine if observed data is significantly different from what would be expected under the null hypothesis.
Can I calculate a P-value for any dataset in Excel?

+
Yes, as long as your dataset meets the assumptions of the statistical test you’re using, Excel provides various functions to calculate P-values for different scenarios.
What does a small P-value mean?
+
A small P-value (typically less than 0.05) suggests that there is a low probability that your results could occur by chance, implying statistical significance.